本記事では不等式について説明する。
不等式を表すときに用いる不等号とは数(もしくは関数)の大小関係を表す記号である。
また、不等号を用いて、変数の範囲を表すこともできる。
いわゆる二次不等式とは最大のべき数が2である不等式のことである。
二次不等式の解は変数の範囲によって表す。
不等式とは
まず、不等号について説明する。
ここで、二つの実数\(a,b\)の大小関係を以下のように書くことができる。
\begin{eqnarray}
&&x＞y\\
&&xはyより大きい。\\
\\
&&x＜y\\
&&xはyより小さい。\\
\\
&&x\geqq y\\
&&xはy以上である。\\
\\
&&x\leqq y\\
&&xはy以下である。
\end{eqnarray}
以上のように二つの実数\(a,b\)の大小関係を不等号を用いて表すことができる。
では、次に関数の大小関係を不等号を用いて表す。
二つの関数\(f(x),g(x)\)の大小関係を書くと以下のように表せる。
\begin{eqnarray}
&&f(x)＞g(x)\\
&&f(x)はg(x)より大きい。\\
\\
&&f(x)＜g(x)\\
&&f(x)はg(x)より小さい。\\
\\
&&f(x)\geqq g(x)\\
&&f(x)はg(x)以上である。\\
\\
&&f(x)\leqq g(x)\\
&&f(x)はg(x)以下である。
\end{eqnarray}
ここで、注意することは二つの関数の大小関係は変数\(x\)によって変化する場合がある。
二つの関数の大小関係が成立する変数\(x\)の範囲を求めることは、不等式の解を求めることと同義である。
関数の不等式
本章では関数の不等式について説明する。
二つの関数の交点が存在する場合と存在しない場合について考える。
交点が存在する
図1.1のように二つの関数\(f(x),g(x)\)がある。
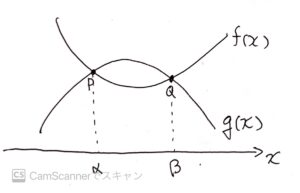図1.1 関数f(x)とg(x)この時、二つの関数の交点を\(x\)が小さい順に\(P,Q\)とし、それらの\(x\)座標を\(\alpha,\beta\)とする。
この時、\(x＜\alpha\)(\(x\)が\(\alpha\)より小さい)の場合、\(g(x)＜f(x)\)である。
だが、\(\alpha＜x＜\beta\)(\(x\)が\(\alpha\)より大きく、\(\beta\)より小さい)場合、\(f(x)＜g(x)\)である。
そして、\(\beta＜x\)(\(x\)が\(\beta\)より大きい)場合、\(g(x)＜f(x)\)となる。
つまり、二つの関数\(f(x),g(x)\)の大小関係は、二つの関数の交点\(P,Q\)の前後で変わっていることが分かる。
二つの関数の大小関係を調べたければ、二つの関数の交点を調べる必要がある。
つまり、以下の等式を満たす\(x\)を具体的に調べる必要がある。
\begin{eqnarray}
f(x)=g(x)
\end{eqnarray}
例)
以下の二つの関数がある。
\begin{eqnarray}
f(x)&=&x^2-3x+3\\
\\
g(x)&=&-2x^2+6x+1
\end{eqnarray}
この時、以下の不等式を満たす\(x\)の範囲を考える。
\begin{eqnarray}
g(x)\leqq f(x)\tag{1.1}
\end{eqnarray}
まず、\(f(x),g(x)\)の交点を調べるために、以下の等式を満たす\(x\)を求める。
\begin{eqnarray}
f(x)=g(x)
\end{eqnarray}
これを整理すると、以下のような二次方程式になる。
\begin{eqnarray}
3x^2-9x+2=0
\end{eqnarray}
この方程式の解は\(x=\frac{9\pm\sqrt{57}}{6}\)である。
ここで、\(\alpha=\frac{9-\sqrt{57}}{6},\beta=\frac{9+\sqrt{57}}{6}\)と方程式の解を表す。
また、\(f(x),g(x)\)の\(x^2\)の係数に注目すると、\(f(x)\)は下に凸の関数であり、\(g(x)\)は上に凸である関数であることが分かる。
よって、二つの関数の関係を描くと図1.2のようになる。
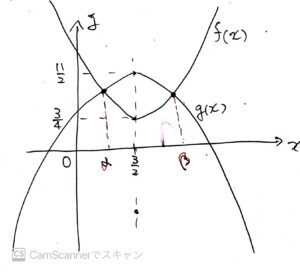図1.2 関数f(x)とg(x)のグラフよって、式\(1.1\)の不等式を満たす\(x\)の範囲は以下になる。\begin{eqnarray}
x\leqq \alpha,\beta\leqq x
\end{eqnarray}
ここで注意することは、ここでは二つの関数の交点が二つであると仮定したが、必ずしも二つであるとは限らない。
交点が存在しない
本節では、二つの関数が交わらない場合を考える。
図1.3のように二つの関数\(f(x),g(x)\)がある。
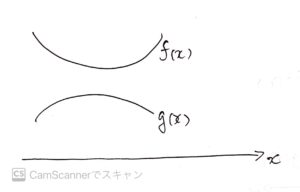図1.3 関数f(x)とg(x)これらの二つの関数は交わらないので、以下の等式の解は虚数解となる。
\begin{eqnarray}
f(x)=g(x)
\end{eqnarray}
虚数解であるということは、二つの関数\(f(x),g(x)\)は交わらないということである。
つまり、二つの関数の大小関係は全ての\(x\)に対して不変である。
ここで、\(x=0\)の時の二つの関数\(f(x),g(x)\)の大小関係を調べる。
ここで、求めた大小関係は全ての\(x\)で成立する。
例)
二つの関数がある。
\begin{eqnarray}
f(x)&=&x^2+2x+3\\
\\
g(x)&=&-2x^2+6x+1
\end{eqnarray}
これらの関数の大小関係が以下である時の\(x\)の範囲を考える。
\begin{eqnarray}
g(x)\leqq f(x)\tag{1.2}
\end{eqnarray}
まず、二つの関数の交点を求める為に、以下の等式を満たす\(x\)を求める。
\begin{eqnarray}
f(x)=g(x)
\end{eqnarray}
この方程式を整理すると以下になる。
\begin{eqnarray}
3x^2-4x+2=0
\end{eqnarray}
この方程式の解は\(x=\frac{4\pm i2\sqrt{2}}{6}\)であり、虚数解である。
つまり、二つの関数\(f(x),g(x)\)は交わらないということを意味し、\(f(x),g(x)\)の大小関係は全ての\(x\)について不変である。
ここで、\(x=0\)の時を考えると、\(f(x=0)=3\leqq g(x=0)=1\)であることが分かる。(図1.4)
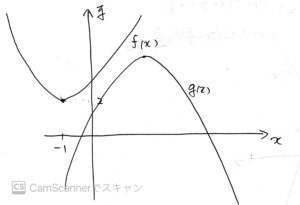図1.4 関数f(x)とg(x)のグラフ全ての\(x\)について、\(f(x),g(x)\)の大小関係は不変なので、全ての\(x\)において\(g(x)\leqq f(x)\)であることが分かる。
よって、式\(1.2\)を満たす\(x\)は全範囲である。
まとめ
本記事では、不等式について説明した。
その内容を以下にまとめる。
- 不等号とは二つの実数、または関数の大小関係を表す記号である。
- 二つの関数\(f(x),g(x)\)の不等式を求めるために、\(f(x)=g(x)\)を満たす\(x\)を求めて、二つの関数の交点を調べる。
- \(f(x)=g(x)\)の解が実数解の場合は、\(f(x),g(x)\)の大小関係が変化する可能性のある交点が存在することを意味しているので、交点の\(x\)座標に注意しながら不等式を満たす\(x\)の範囲を求める。
- \(f(x)=g(x)\)の解が虚数解の場合は、\(f(x),g(x)\)の大小関係は不変なので、ある一つの\(x\)についての\(f(x),g(x)\)の大小関係を調べることで求めることができる。
関数を考える時は、グラフに描いて考えると分かりやすい。
この時、関数の交点の有無と関数の概形(上下のどちらに凸かなど)に注意して描くことが大切である。
演習問題
二つの関数がある。
\begin{eqnarray}
&&f(x)=x^2-2ax+a^2-5\\
\\
&&g(x)=-x^2+4x-8\\
\\
&&a:定数
\end{eqnarray}
以上の二つの関数についての不等式を解け。
\begin{eqnarray}
g(x)＞f(x)\tag{5.1}
\end{eqnarray}
等式より、以下の関係が成立する。
\begin{eqnarray}
&&x^2-2ax+a^2-5=-x^2+4x-8\\
\\
&&2x^2-2\left(a+2\right)x+a^2+3=0\tag{5.2}
\end{eqnarray}
以上の方程式の解は以下である。
\begin{eqnarray}
x=a+2\pm\sqrt{-a^2+4a-2}
\end{eqnarray}
この解は定数\(a\)の値によって実数解を持つか、虚数解を持つかが変わる。
ここで、\(D=-a^2+4a-2\)と置き、\(a\)によって変化する\(D\)の正負を考える。
まず、\(D=0\)を考えると以下の等式を満たす。
\begin{eqnarray}
a^2-4a+2=0
\end{eqnarray}
この方程式を満たす\(a\)は以下である。
\begin{eqnarray}
a=2\pm\sqrt{2}
\end{eqnarray}
また、図のように縦軸\(D\)、横軸\(a\)としてグラフを書いてみると、\(D\)は下に凸であるグラフと分かる。
よって、\(D\)の正負は以下の\(a\)の範囲によって決まる。
\begin{eqnarray}
&&D＞0:&2-\sqrt{2}＜a＜2+\sqrt{2}\\
\\
&&D=0:&a=2\pm\sqrt{2}\\
\\
&&D＜0:&a＜2-\sqrt{2},2+\sqrt{2}＜a
\end{eqnarray}
以上のような\(D\)の正負を考えながら、式\(5.2\)の解と不等式について考える。
\(D＜0\)の場合の解は虚数解を持つので、二つの関数\(f(x),g(x)\)は交点を持たない。
つまり、\(f(x),g(x)\)の大小関係は全ての\(x\)について不変である。
ここで、\(x=0\)の場合を考えてみると、\(f(x=0)=a^2-5＞g(x=0)=-8\)を満たす。
よって、全ての\(x\)について\(f(x)＞g(x)\)を満たす。
だが、これは式\(5.1\)を満たさない。
よって、\(D＜0\)の場合、つまり、\(a＜2-\sqrt{2},2+\sqrt{2}＜a\)の場合は不等式\(5.1\)を満たさない。
次に、\(D=0\)の場合を考える。
\(D=0\)では式\(5.2\)の解は一つになり、\(a=2+\sqrt{2}\)の時、\(x=4+\sqrt{2}\)となり、\(a=2-\sqrt{2}\)の時、\(x=4-\sqrt{2}\)となる。
つまり、\(f(x),g(x)\)はそれぞれの\(a\)において\(x=4\pm\sqrt{2}\)で交わってることになる。
では、この交点の前後での\(f(x),g(x)\)の大小関係について調べる。
まず、\(a=2+\sqrt{2}\)の場合について考える。
\(x=4+\sqrt{2}\)の前後を考えるので、\(x=0\)と\(x=6\)の時の\(f(x),g(x)\)の大小関係を調べると以下になる。
\begin{eqnarray}
&&f(x=0)=1+4\sqrt{2}＞g(x=0)=-8\\
\\
&&f(x=6)=9-8\sqrt{2}＞g(x=6)=-16
\end{eqnarray}
よって、\(a=2+\sqrt{2}\)の時は\(f(x),g(x)\)の大小関係は常に\(f(x)＞g(x)\)である。
次に\(a=2-\sqrt{2}\)の場合について考える。
\(x=4-\sqrt{2}\)の前後を考えるので、\(x=0\)と\(x=3\)の時の\(f(x),g(x)\)の大小関係を調べると以下になる。
\begin{eqnarray}
&&f(x=0)=1-4\sqrt{2}＞g(x=0)=-8\\
\\
&&f(x=3)=-2-\sqrt{2}＞g(x=3)=-5
\end{eqnarray}
よって、\(a=2+\sqrt{2}\)の時も\(f(x),g(x)\)の大小関係は常に\(f(x)＞g(x)\)である。
以上の事から、\(D=0\)の時も不等式\(5.1\)は満たさない。
最後に、\(D＞0\)の時を考える。
すると、式\(5.2\)の解は実数解を二つ持つことになるので、二つの関数\(f(x),g(x)\)の交点は二つ存在することになる。
ここで、式\(5.2\)の二つの解をそれぞれ以下のように置く。
\begin{eqnarray}
\alpha&=&a+2-\sqrt{-a^2+4a-2}\\
\\
\beta&=&a+2+\sqrt{-a^2+4a-2}
\end{eqnarray}
図に描くと、\(f(x)\)は下に凸であり、\(g(x)\)は上に凸なので図のようになる。
よって、不等式\(5.1\)を満たす\(x\)の範囲は\(\alpha＜x＜\beta\)である。
以上のことをまとめると、不等式\(5.1\)の解は定数\(a\)によって変化し、\(a\)が以下のような範囲を取る時、不等式\(5.1\)の解は以下になる。
\begin{eqnarray}
&&\alpha＜x＜\beta\\
\\
&&(2-\sqrt{2}＜a＜2+\sqrt{2})
\end{eqnarray}
