三角比とは
直角三角形の辺の比
三角比とは直角三角形の比の事である。
三角比は言葉のようにsin(サイン)、cos(coコサイン)、tan(タンジェント)の3つある。
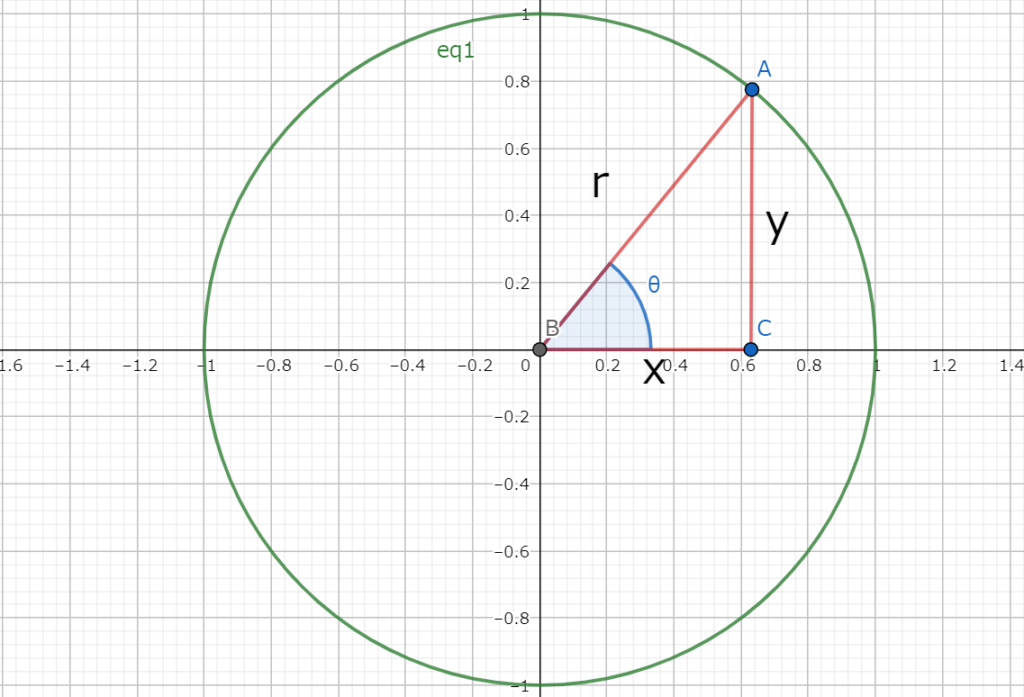図1．r、x、yで表す直角三角形図1を例とすると、三角比は以下になる。
$$\sinθ=\frac{y}{r}\\
\cosθ=\frac{x}{r}\\
\tanθ=\frac{y}{x}$$
単位円を使って考える三角比
三角比は単位円を使って考えるとより正確に理解できる。
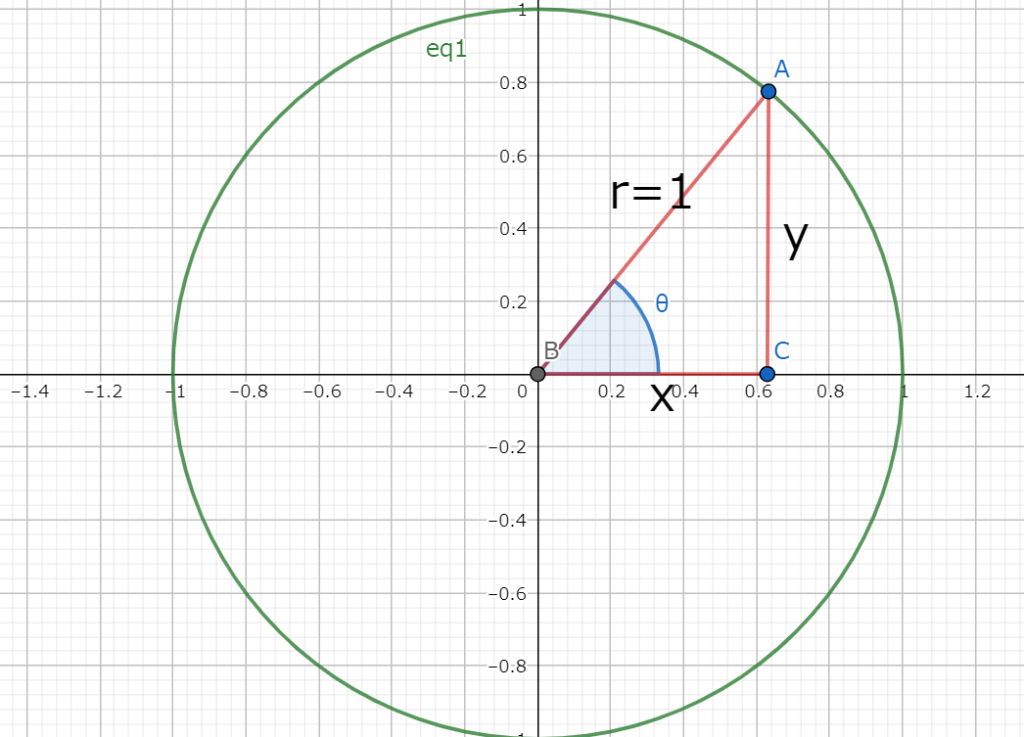図2．半径が1の単位円単位円とは図2のように半径が1の円のことである。
図2のような単位円上にある点Aを考える。
点Aの座標をxとy、原点Oからの距離をrとすると自然と直角三角形ができて、三角比を満たすようになる。
また、単位円で考えるとxとyは負の値も取るようになる。
なので、三角比おいても負の値を考えるようになる。
xが負の値を取る時はcosは負の値を取り、yが負の値を取る時はsinは負の値を取る。
角度で考えると角度が90°以上になるとcosは負の値を取り始め、180°を超えるとsinが負の値を取り始める。
sin、cosの正負の関係は以下になる。
\begin{eqnarray}
\sinθ>0&;&0°< θ <180°\\
\sinθ<0&;&180°< θ <360°\\
\cosθ>0&;&0°< θ <90°,270°< θ <360°\\
\cosθ<0&;&90°< θ <270°
\end{eqnarray}
覚えておくべき三角比
三角比の値を全て覚えることは不可能である。
だが、有名で分かりやすい三角比は覚えておく必要がある。
30°、60°
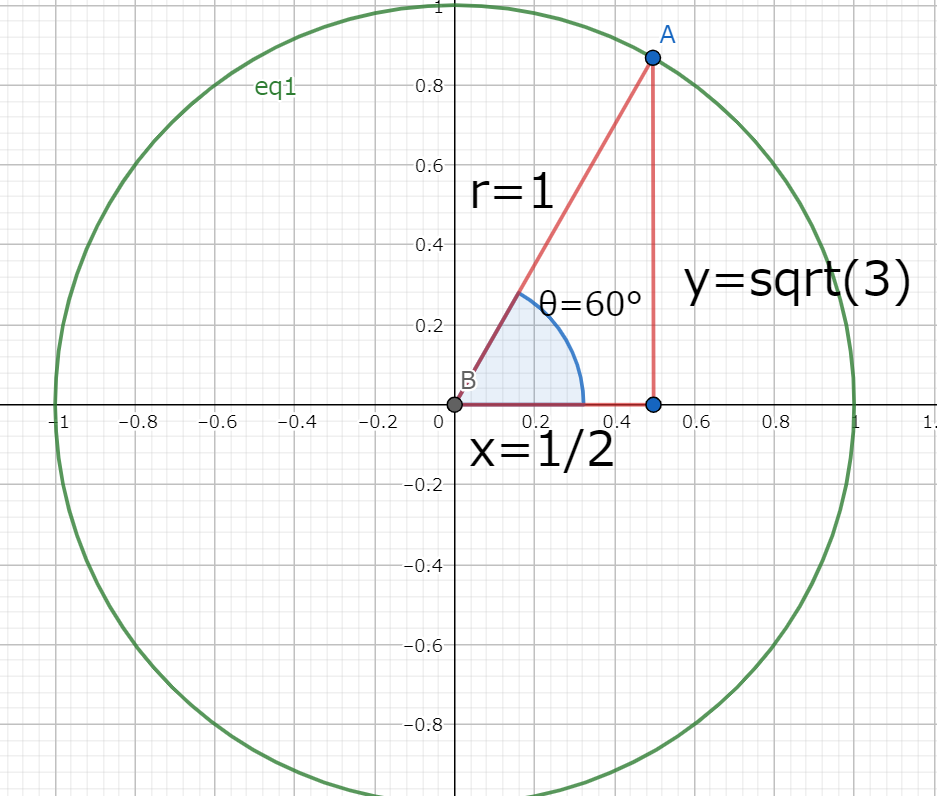図3．角度θが60°の時の直角三角形
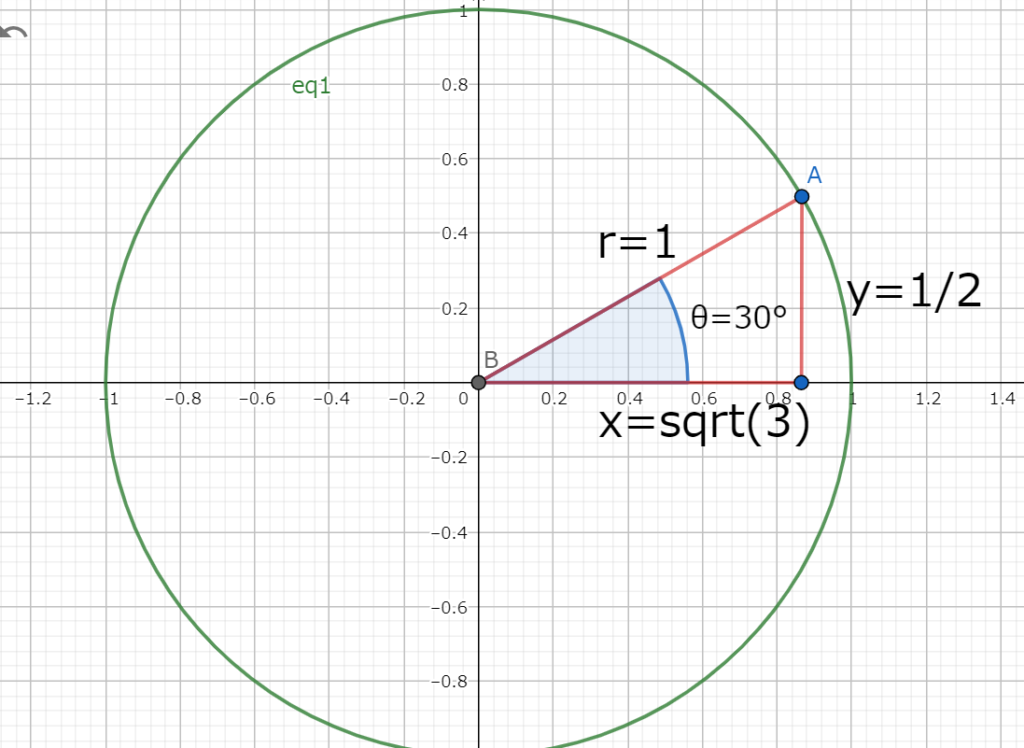図4．角度θが30°の時の直角三角形図3のように直角以外の角度が30°、60°になっている直角三角形の比は以下になる。
$$\sin30°=\frac{1}{2}\\
\cos30°=\frac{\sqrt{3}}{2}\\
\tan30°=\frac{1}{\sqrt{3}}\\
\sin60°=\frac{\sqrt{3}}{2}\\
\cos60°=\frac{1}{2}\\
\tan60°=\sqrt{3}$$
45°
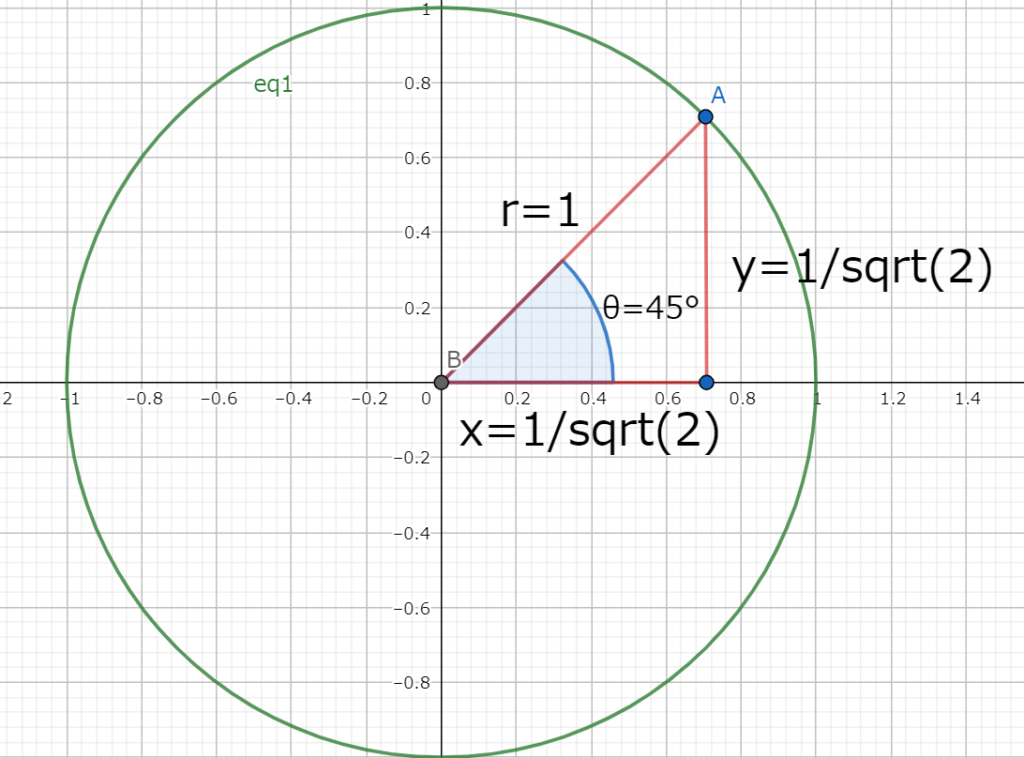図5.θが45°の二等辺直角三角形図5のように二等辺直角三角形の三角比は以下になる。
$$\sin45°=\cos45°=\frac{\sqrt{2}}{1}\\
\tan45°=1$$
三角比の公式
三角比sin,cos,tanの間にはある関係がある。
それを公式をして理解することで三角比を変換をすることもできる。
(例えばsinからcosに変換するなど)
$$\sin^{2}θ+\cos^{2}θ=1$$
非常によく使うのはこの公式である。
この公式は図2の単位円を考えると分かりやすい。
単位円を考えると三角比は以下になる。
$$\sinθ=y\\
\cosθ=x$$
以上のことからパスカルの定理を使うと、
$$x^2+y^2=1$$
より、
$$\sin^{2}θ+\cos^{2}θ=1$$
となる。
$+\tan^{2}=\frac{1}{\cos^{2}θ}$$
この公式はsin,cosからtanに変換する時に良く使われる。
この公式は前節の$$\sin^{2}θ+\cos^{2}θ=1$$から導かれる。
まず、両辺を$$\cos^{2}θ$$で割る。
すると、
$$\frac{\sin^{2}θ}{\cos^{2}θ}+1=\frac{1}{\cos^{2}θ}$$
となる。
ここで、
$$\tanθ=\frac{\sinθ}{\cosθ}$$
という関係を使う。
単位円を考えるとこのことは分かる。
よって、
$$1+\tan^{2}θ=\frac{1}{\cos^{2}θ}$$
の公式が導かれるのである。
【練習問題はこちら】
