問題
問1
以下の関数のグラフを書き、またその軸と頂点を求めよ。
$$y=2x^2-6x+3$$
問2
以下の放物線の座標が以下の座標にある時、定数a,bを求めよ。
$$放物線y=\frac{1}{2}x^2+ax+b$$
$$座標\left(\frac{3}{2},-\frac{9}{4}\right)$$
問3
以下の放物線をx軸方向に1、y軸方向に-3平行移動した後の放物線の方程式を求めよ。
$$y=2x^2-4x+3$$
問4
ある放物線をx軸方向に-2、y軸方向に-2平行移動し、更に原点に関して対称移動すると以下の放物線に移った。
$$y=-x^2+x-8\tag{式4.1}$$
元の放物線の方程式を求めよ。
【二次関数の解説】
解答
問1の解答 平方完成をする
最初に方程式を平方完成する。
つまり、方程式を以下の形に直すということである。
$$y=a\left(x-p\right)^2+q$$
まず、xを含む最初の2項目までをx^2の係数である2で因数分解する。
すると、以下の様になる。
$$y=2\left(x^2-3x\right)+3$$
ここで、かっこの中に以下の数を足す。
$$\frac{9}{4}-\frac{9}{4}$$
すると、かっこの中を因数分解することができる。
因数分解すると以下の様になる。
$$y=2\left(\left(x-\frac{3}{2}\right)^2-\frac{9}{4}\right)+3$$
最後にかっこの中の9/4をかっこの外に出す。
すると、以下の様に平方完成が完成する、
$$y=2\left(x-\frac{3}{2}\right)^2-\frac{3}{2}$$
ここで、グラフは図1.1のようになる。
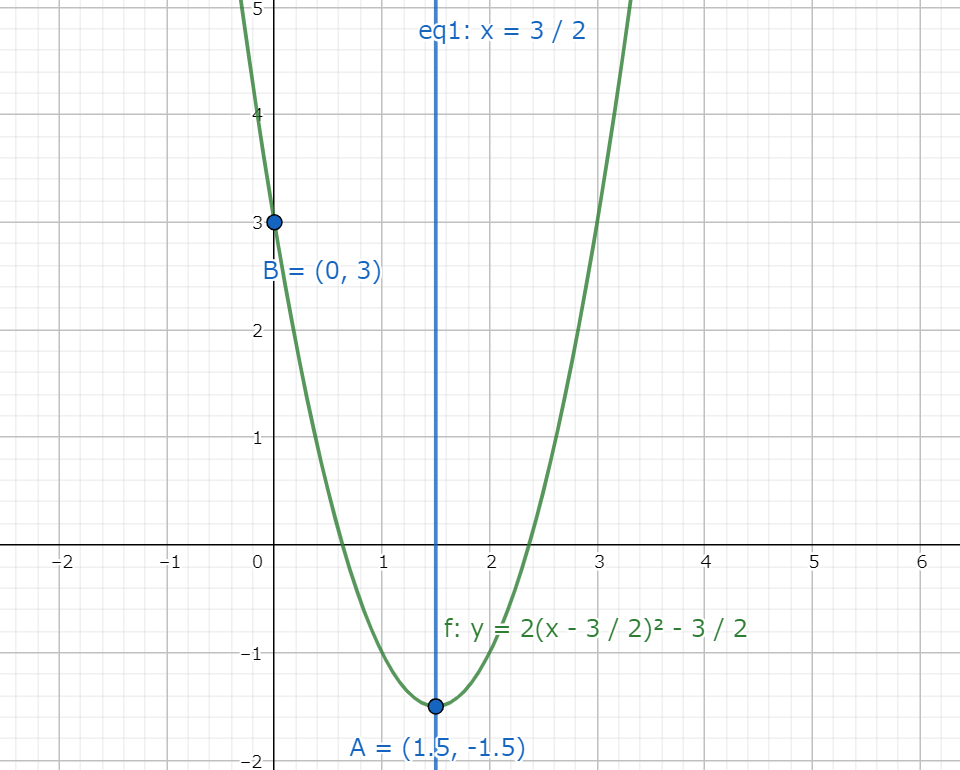 図1.1 平方完成した放物線の方程式と軸のグラフ
図1.1 平方完成した放物線の方程式と軸のグラフ軸と頂点は以下の様になる。
\begin{eqnarray}
軸&:&x=\frac{3}{2}\\
頂点&:&\left(\frac{3}{2},-\frac{3}{2}\right)
\end{eqnarray}
よって、グラフと軸と頂点を求めることができた。
問2の解答 文字のまま平方完成をする
最初に放物線の方程式を文字が入ったまま平方完成をする。
まず、xを含んだ2項目までを1/2でくくる。
すると、以下の様になる。
$$y=\frac{1}{2}\left(x^2+2ax\right)+b$$
次に、かっこの中にa^2-a^2を足す。
すると、かっこの中を因数分解することができる。
因数分解すると以下の様になる。
$$y=\frac{1}{2}\left(\left(x+a\right)^2-a^2\right)+b$$
最後に-a^2をかっこの外に出す。
すると、以下の様になる。
$$y=\frac{1}{2}\left(x+a\right)^2-\frac{1}{2}a^2+b$$
この時、頂点は以下の値を取る。
$$\left(\frac{3}{2},-\frac{9}{4}\right)$$
よって、式2.1から以下の関係が成り立つ。
\begin{eqnarray}
a=-\frac{3}{2}\\
-\frac{1}{2}a^2+b=-\frac{9}{4}
\end{eqnarray}
よって、定数a,bの値は以下の様になる。
\begin{eqnarray}
a=\frac{3}{2}\\
b=\frac{9}{8}
\end{eqnarray}
よって、定数a,bを求めることができた。
問3の解答 平方完成をして頂点を求めてから移動
最初に放物線の方程式を平方完成する。
まず、xを含む最初の2項目までを2でくくる。
すると、以下の様になる。
$$y=2\left(x^2-2x\right)+3$$
次にかっこの中に1-1を足す。
すると、かっこの中を因数分解することができる。
因数分解すると以下の様になる。
$$y=2\left(\left(x-1\right)^2-1\right)+3$$
最後にかっこの中の-1をかっこの外に出す。
すると、以下の様に平方完成ができる。
$$y=2\left(x-1\right)^2+1$$
この放物線をx軸方向に1、y軸方向に-3平行移動する。
つまり、頂点をx軸方向に1、y軸方向に-3だけずらすということである。
つまり、平行移動させた後の放物線の方程式は以下の様になる。
$$y=2\left(x-2\right)^2-2$$
よって、平行移動させた放物線の方程式を求めることができた。
グラフは図3.1になる。
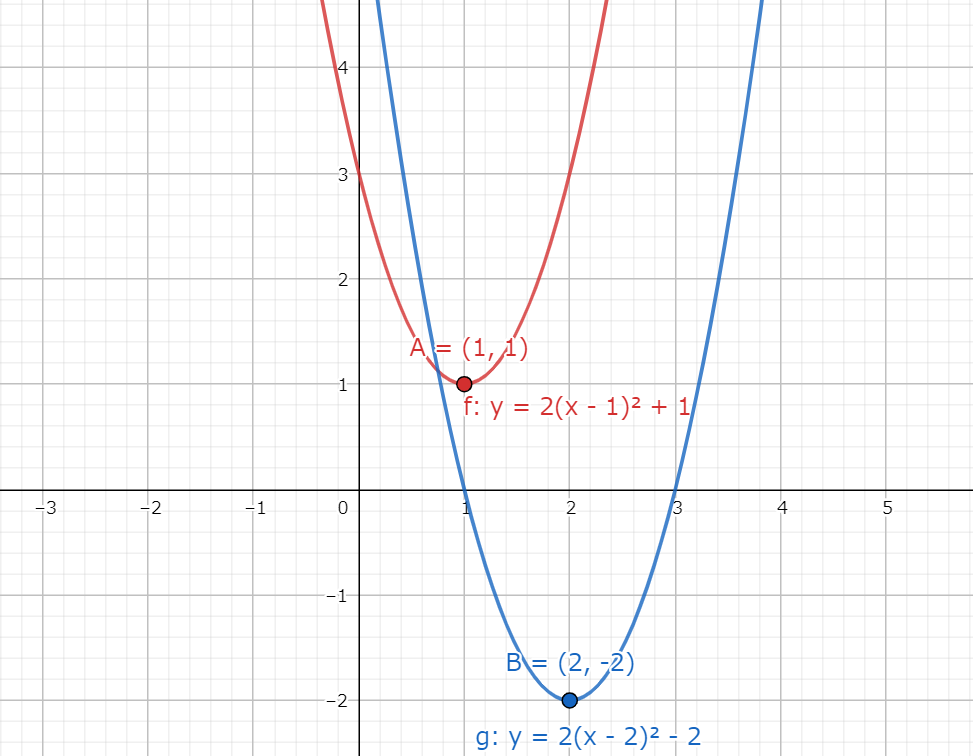 図3.1 平行移動する前の放物線と平行移動させた後の放物線
図3.1 平行移動する前の放物線と平行移動させた後の放物線問4の解答 移動した後の方程式を平方完成してから逆に移動させる
この問題は操作した後の放物線の式4.1を逆の操作をして元の放物線を求める。
最初に式4.1を平方完成する。
まず、xを含む最初の2項目までを-1でくくる。
すると、以下の様になる。
$$y=-\left(x^2-x\right)-8$$
次にかっこの中に1/4-1/4を足す。
すると、かっこの中を因数分解することができる。
因数分解すると以下の様になる。
$$y=-\left(\left(x-\frac{1}{2}\right)^2-\frac{1}{4}\right)-8$$
最後にかっこの中の-1/4をかっこの外に出す。
すると、以下の様に平方完成することができる。
$$y=-\left(x-\frac{1}{2}\right)^2-\frac{31}{4}$$
次に平方完成した放物線を原点に対して対称移動させる。
つまり、放物線を原点を中心に鏡のように反転させる。
方程式の操作としてはxとyにそれぞれ-1をかける。
よって、放物線の方程式は以下の様になる。
$$y=\left(x+\frac{1}{2}\right)^2+\frac{31}{4}$$
グラフは図4.1になる。
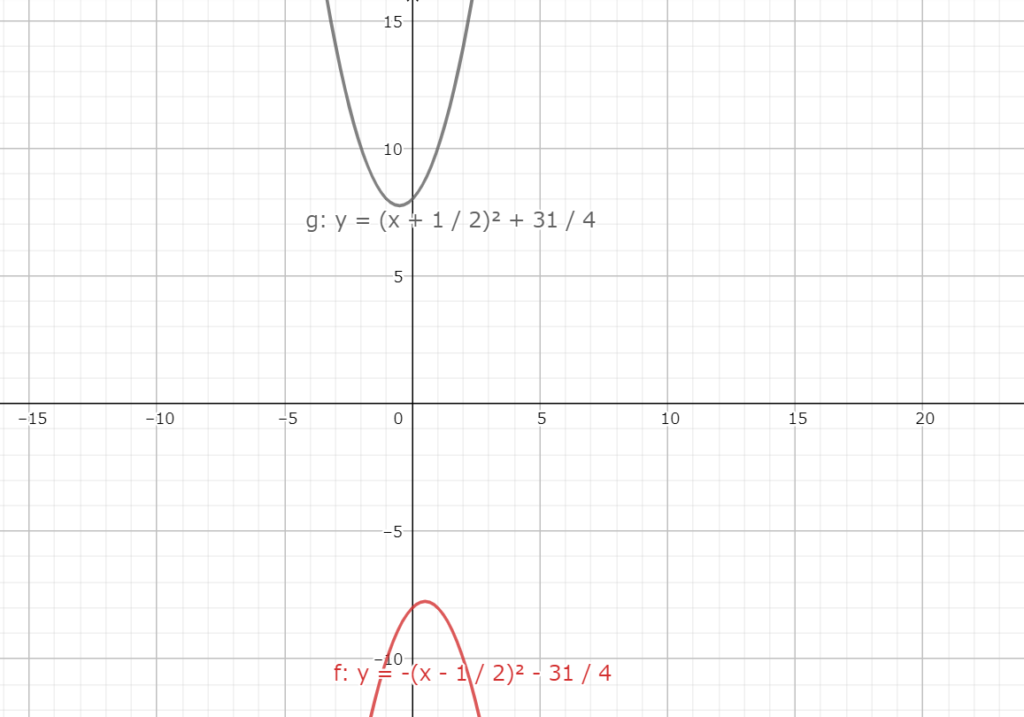 図4.1 放物線を原点を中心として対称移動させた後の放物線(グレー)
図4.1 放物線を原点を中心として対称移動させた後の放物線(グレー)次に元の放物線に操作した平行移動の逆を行うので、x軸方向に2、y軸方向に2だけ平行移動させる。
すると、放物線の方程式は以下の様になる。
$$y=\left(x-\frac{3}{2}\right)^2+\frac{39}{4}$$
よって、元の放物線の方程式を求めることができた。
グラフは図4.2になる。
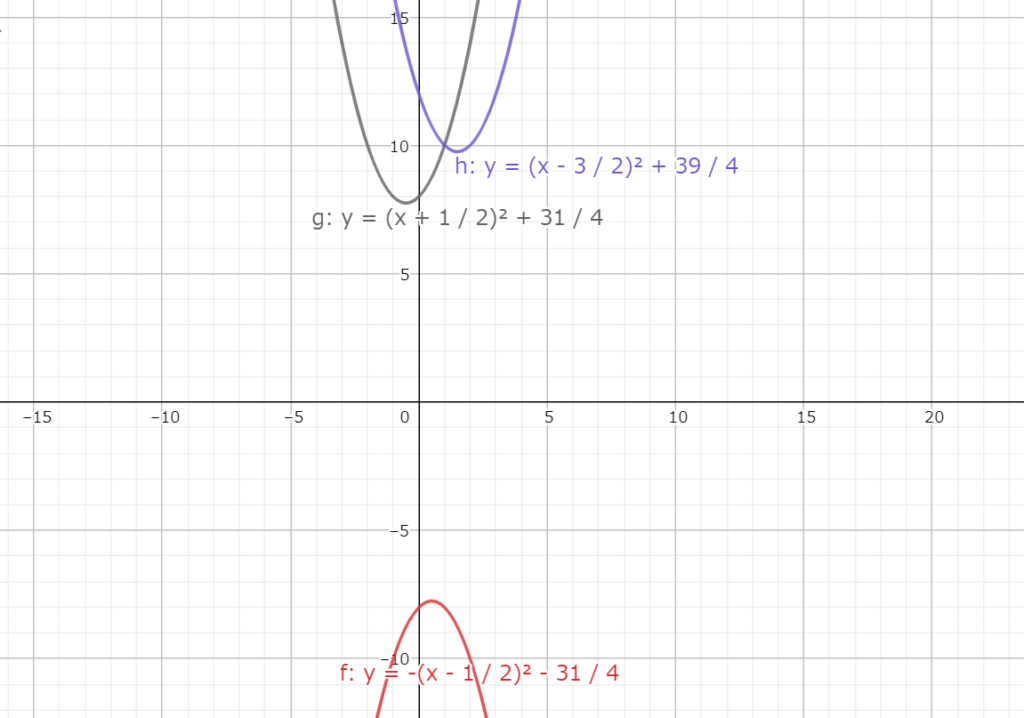 図4.2 放物線を平行移動させた後の放物線(青)
図4.2 放物線を平行移動させた後の放物線(青)【二次関数の解説】

