問題
問1
2点\((2,0),(-2,0)\)を焦点として、長軸の長さが6である楕円の方程式を求めよ。
【解答はこちら】
問2
点\(A(\sqrt{3},0)\)と準線\(x=\frac{4}{\sqrt{3}}\)からの距離の比が\(\sqrt{3}:2\)である点\(P(x,y)\)の軌跡を求めよ。
【解答はこちら】
問3
以下の放物線の極方程式を求めよ。
\begin{eqnarray}
x^2=-6y+9
\end{eqnarray}
【解答はこちら】
問4
以下の曲線の外形を描け。
\begin{eqnarray}
r=\frac{1}{\sqrt{2}-\sin\theta}\tag{4.1}
\end{eqnarray}
【解答はこちら】
問5
以下の放物線がある。
\begin{eqnarray}
y^2=4px
\end{eqnarray}
この放物線上に4つの点があり、y座標が大きい順にA,B,C,Dとする。
この時、線分ACとBDは放物線の焦点Fで垂直に交わっている。
ベクトル\(\overrightarrow{FA}\)が\(x\)軸の正の方向となす角を\(\theta\)とする。
(1)
AFの長さを\(p,\theta\)を用いて表わせ。
(2)
以下の値は\(\theta\)に依らず、一定であることを示せ。
\begin{eqnarray}
\frac{1}{AF\cdot CF}+\frac{1}{BF\cdot DF}\tag{5.1}
\end{eqnarray}
【解答はこちら】
解答
問1の解答 \(x=0\)の時の\(y\)を求めて短軸を求める
【問題はこちら】
楕円上にある点を\(P(x,y)\)とする。
この時、点Pは以下の関係を満たす。
\begin{eqnarray}
\sqrt{\left(x-2\right)^2+y^2}+\sqrt{\left(x+2\right)^2+y^2}=6\tag{1.1}
\end{eqnarray}
ここで、式1.1において\(x-0\)の時の\(y\)を求めることで楕円の短軸を求めることができる。
式1.1において\(x=0\)の時、以下の様になる。
\begin{eqnarray}
\sqrt{4+y^2}+\sqrt{4+y^2}&=&6\\
\\
\sqrt{4+y^2}&=&3\\
\\
y^2&=&5
\end{eqnarray}
よって、楕円の方程式は以下となる。
\begin{eqnarray}
\frac{x^2}{9}+\frac{y^2}{5}=1
\end{eqnarray}
問2の解答 離心率\(e<1\)より楕円の軌跡であることを予想する
【問題はこちら】
点Pと焦点Aとの距離\(PA\)は以下のようにかける。
\begin{eqnarray}
PA=\sqrt{\left(x-\sqrt{3}+y^2\right)}
\end{eqnarray}
また、点Pと準線との距離\(d\)は以下のようにかける。
\begin{eqnarray}
d=|x-\frac{4}{\sqrt{3}}|
\end{eqnarray}
よって、\(PA\)と\(d\)の比は以下の様になる。
\begin{eqnarray}
\frac{PA}{d}&=&\frac{\sqrt{\left(x-\sqrt{3}\right)^2+y^2}}{|x-\frac{4}{\sqrt{3}}|}\\
\\
&=&\frac{\sqrt{3}}{2}
\end{eqnarray}
ここで、\(\frac{PA}{d}\)は離心率\(e<1\)であるのでであるので求める軌跡は楕円の方程式であることが分かる。
ここで、離心率を展開していくと以下の様になる。
\begin{eqnarray}
\sqrt{\left(x-\sqrt{3}\right)^2+y^2}&=&\frac{\sqrt{3}}{2}|x-\frac{4}{\sqrt{3}}|\\
\\
\left(x-\sqrt{3}\right)+y^2&=&\frac{3}{4}\left(x-\frac{4}{\sqrt{3}}\right)\\
\\
\frac{x^2}{4}+y^2=1
\end{eqnarray}
よって、長軸が4、短軸が2の楕円の軌跡となる。
問3の解答 \(x,y\)を極座標で表して\(\sin\theta\)の2次方程式を解く
【問題はこちら】
\(x,y\)を極座標で以下のように置く。
\begin{eqnarray}
x&=&\cos\theta\\
\\
y&=&\sin\theta
\end{eqnarray}
よって、放物線の方程式は以下の様になる。
\begin{eqnarray}
r^2\cos^2\theta=-6r\sin\theta+9
\end{eqnarray}
ここで、\(\cos^2\theta=1-\sin\theta\)を使って\(\sin\theta\)だけの式に変形する。
\begin{eqnarray}
r^2\left(1-\sin^2\theta\right)=-6\sin\theta+9\\
\\
r^2\sin^2\theta-6r\sin\theta-r^2+9=0\\
\\
\left(r\sin\theta+r-3\right)\left(r\sin\theta-r-3\right)=0
\end{eqnarray}
よって、\(\sin\theta\)の2次方程式を作り解くことができる。
\(\sin\theta\)は以下の値を取る。
\begin{eqnarray}
\sin\theta=1-\frac{3}{r},1+\frac{3}{r}
\end{eqnarray}
だが、ここで\(-1\leq\sin\theta\leq1\)なので、\(\sin\theta=1-\frac{3}{r}\)の値のみを取る。
よって、\(r=\)の式に直すと以下のように極方程式を求めることができる。
\begin{eqnarray}
r=\frac{3}{1+\sin\theta}
\end{eqnarray}
問4の解答 極座標表示からデカルト座標表示に変換する
【問題はこちら】
式4.1を式変形すると以下の様になる。
\begin{eqnarray}
\sqrt{2}r-r\sin\theta=1
\end{eqnarray}
ここで、\(r,θ\)を以下の関係を満たすとする。
\begin{eqnarray}
x=r\cos\theta\\
\\
y=r\sin\theta
\end{eqnarray}
よって、式4.1は以下のように極座標表示からデカルト座標表示に式変形できる。
\begin{eqnarray}
\sqrt{2x^2+2y^2}+y=1\\
\\
2x^2+2y^2=\left(1-y\right)^2\\
\\
2x^2+2y^2=1-2y+y^2\\
\\
2x^2+y^2+2y=1\\
\\
2x^2+\left(y+1\right)^2=2\\
\\
x^2+\frac{\left(y+1\right)^2}{2}=1
\end{eqnarray}
よって、以上の方程式はy軸方向に伸びている長軸が\(2\sqrt{2}\)で中心が\((0,1)\)の楕円であることが分かる。
よって、図4.1のようなグラフを描くことができる。
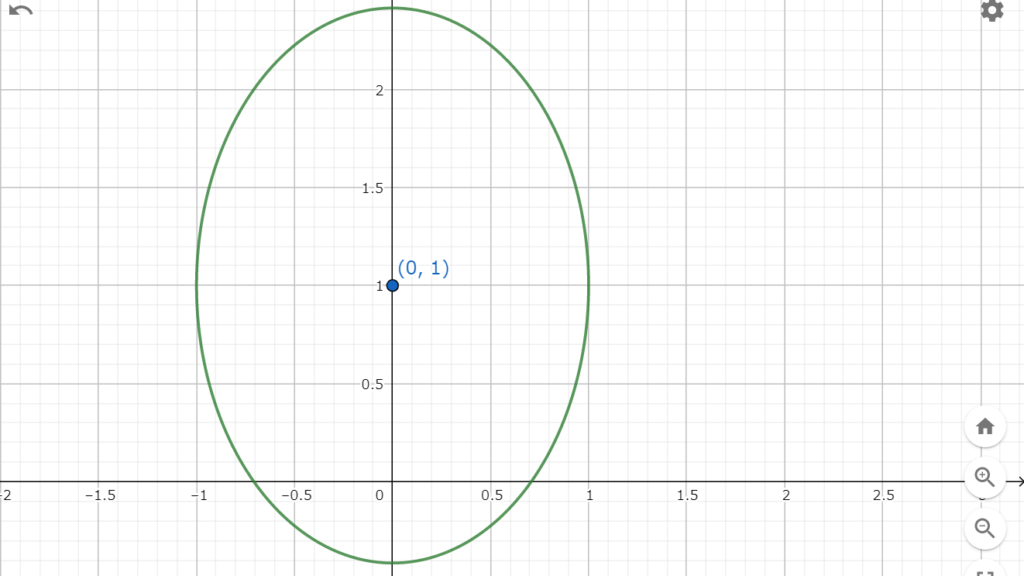 図4.1 長軸が√2の楕円
図4.1 長軸が√2の楕円問5の解答 AFを\(f(p,\theta)\)と置いて\(f(p,\theta)を求める\)
【問題はこちら】
(1)
ここで、\(A=(A_x,A_y)\)と置く。
この時、\(A_x,A_y\)はそれぞれ以下のように求めることができる。
\begin{eqnarray}
A_x&=&f(p,\theta)\cos\theta+p=\frac{A_y^2}{4p}\\
\\
A_y&=&f(p,\theta)\sin\theta
\end{eqnarray}
ここで、AFを\(p\)と\(\theta\)の関数\(f(p,\theta)\)と置いた。
よって、以下のような\(p,\theta\)の方程式を作ることができる。
\begin{eqnarray}
f(p,\theta)\cos\theta+p=\frac{\left(f(p,\theta)\sin\theta\right)^2}{4p}
\end{eqnarray}
これを\(\cos\theta\)の二次方程式に式変形すると以下の様になる。
\begin{eqnarray}
f(p,\theta)^2\cos^2\theta+4pf(p,\theta)\cos\theta+4p^2-f(p,\theta)^2=0\\
\\
\left(f(p,\theta)\cos\theta+2p+f(p,\theta)\right)\left(f(p,\theta)\cos\theta+2p-f(p,\theta)\right)=0
\end{eqnarray}
ここで、\(-1\leq\cos\theta\leq1\)なので\(\cos\theta\)は以下のような値を取る。
\begin{eqnarray}
\cos\theta=1-\frac{2p}{f(p,\theta)}
\end{eqnarray}
よって、これを\(f(p,\theta)\)の式に直すと以下のようになるのでAFの長さを求めることができた。
\begin{eqnarray}
f(p,\theta)=\frac{2p}{1+\cos\theta}
\end{eqnarray}
(2)
ACとBDが点Fで垂直に交わっていることと、y座標の大きい順がA,B,C,Dであるということから\(\overrightarrow{FB},\overrightarrow{FC},\overrightarrow{FD}\)がそれぞれx軸とのなす角は\(\theta+\frac{\pi}{2},\theta+\pi,\theta+\frac{3}{2}\pi\)であることが分かる。
つまり、\(BF,CF,DF\)の長さはそれぞれ以下の様になる。
\begin{eqnarray}
BF&=&\frac{2p}{1+\cos\left(\theta+\frac{\pi}{2}\right)}\\
\\
CF&=&\frac{2p}{1+\cos\left(\theta+\pi\right)}\\
\\
DF&=&\frac{2p}{1+\cos\left(\theta+\frac{3}{2}\pi\right)}
\end{eqnarray}
また、加法定理から以下の関係が成り立つ。
\begin{eqnarray}
\cos\left(\theta+\frac{\pi}{2}\right)&=&-\sin\theta\\
\\
\cos\left(\theta+\pi\right)&=&-\cos\theta\\
\\
\cos\left(\theta+\frac{3}{2}\pi\right)&=&\sin\theta
\end{eqnarray}
よって、\(BF,CF,DF\)は以下の様になる。
\begin{eqnarray}
BF&=&\frac{2p}{1-\sin\theta}\\
\\
CF&=&\frac{2p}{1-\cos\theta}\\
\\
DF&=&\frac{2p}{1+\sin\theta}
\end{eqnarray}
よって、式5.1は以下の様になる。
\begin{eqnarray}
(5.1)&=&\frac{\left(1+\cos\theta\right)\left(1-\cos\theta\right)}{4p^2}+\frac{\left(1-\sin\theta\right)\left(1+\sin\theta\right)}{4p^2}\\
\\
&=&\frac{1-\cos^2\theta+1-\sin^2\theta}{4p^2}\\
\\
&=&\frac{\sin^2\theta+\cos^2\theta}{4p^2}\\
\\
&=&\frac{1}{4p^2}
\end{eqnarray}
よって、式5.1は\(\theta\)に依らず一定である。

