本記事では極限について説明する。
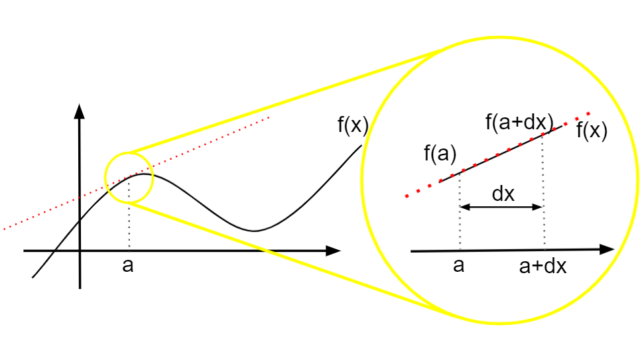
極限とはある関数\(f(x)\)の変数\(x\)をある値\(a\)に限りなく近づける操作である。
この極限の操作によって、関数\(f(x)\)はどのような値を取るのか調べることが極限を学ぶ上で重要である。
極限は微分を学ぶ上でも重要な考え方になるので、ぜひ理解してほしい。
極限とは
極限とは変数\(x\)によって決まる任意の関数\(f(x)\)について、\(x\)をある値\(a\)に近づける操作のことである。
\(x\)をある値\(a\)に近づけることを”極限を取る”と言う。
様々な関数の極限
本節では、どのような関数の極限を取ると、どのような値になるのか見ていく。
\(f(x)=e^{x}\)
まず、\(x\)を\(0\)に近づけた時の関数\(f(x)\)を考える。
これは、当然のように\(f(x)\)は\(1\)に近づくことが分かる。
これを以下のように表記する。
\begin{eqnarray}
\lim_{x \to 0}e^{x}=1
\end{eqnarray}
次に、\(x\)を限りなく大きくする。
(\(x\)を限りなく大きくすることを\(\infty\)に取ると言う。)
\(x\)を\(\infty\)に取ると、\(f(x)\)は限りなく大きくなる(\(\infty\)を取る)ことが分かる。
よって、以下のように表記する。
\begin{eqnarray}
\lim_{x \to \infty}e^{x}=\infty
\end{eqnarray}
このように極限値がある一定の値を取らず、\(\infty\)を取る時、”関数\(f(x)\)は\(x→\infty\)によって発散する”と言う。
次に\(x\)を限りなく小さくする。
(\(x\)を限りなく小さくすることを\(-\infty\)に取ると言う。)
\(x\)を\(-\infty\)に取ると、\(f(x)\)は\(0\)に近づくことが分かる。
よって、以下のように表記する。
\begin{eqnarray}
\lim_{x \to -\infty}e^{x}=0
\end{eqnarray}
このように、極限値がある一定の値を取る時、”関数\(f(x)\)は収束する”と言う。
また、この時の極限値を収束値とも呼ぶ。
\(f(x)=\tan x\)
\(x\)を\(\frac{\pi}{2}\)に限りなく近づける極限を考える。
ここで、図1を見てもらうと分かるように、\(x<\frac{\pi}{2}\)から近づける場合と、\(x>\frac{\pi}{2}\)から近づける場合で、極限値が異なる。
\(x<\frac{\pi}{2}\)から近づけることを\(-x→\frac{\pi}{2}\)と書いて、\(x>\frac{\pi}{2}\)から近づけることを\(+x→\frac{\pi}{2}\)と書く。
これらの事から、関数\(f(x)=\tan x\)の極限値は以下になる。
\begin{eqnarray}
\lim_{-x \to \frac{\pi}{2}}&=&+\infty\\
\\
\lim_{+x \to \frac{\pi}{2}}&=&-\infty
\end{eqnarray}
\(f(x)=\sin x\)
\(x\)を限りなく大きくしても(もしくは小さくしても)、\(\sin x\)は周期関数なので発散もせず、収束もしない。
よって、関数\(f(x)=\sin x\)において、\(x→\pm\infty\)の極限をとっても、極限値は存在しない。
極限値のまとめ
任意の関数\(f(x)\)に関数の極限\(x→a\)を取ると以下のいずれかになる。
\begin{eqnarray}
\lim_{\pm x \to a}f(x)=\begin{cases}
\pm\infty & 発散する\\
\\
\alpha & 収束する\\
\\
極限値は存在しない
\end{cases}
\end{eqnarray}
また、必ずしも
\begin{eqnarray}
\lim_{+x \to a}f(x)=\lim_{-x \to a}f(x)
\end{eqnarray}
ではない。
極限の定理
本章では、極限の定理について2つ説明する。
はさみうちの原理
はさみうちの原理は以下になる。
\begin{eqnarray}
f_1(x)\leqq f_2(x)\leqq f_3(x)\\
\\
\lim_{x \to a}f_1(x)=\lim_{x \to a}f_3(x)=\alpha
\end{eqnarray}
を満たす時、以下のことが言える。
\begin{eqnarray}
\lim_{x \to a}f_2(x)=\alpha
\end{eqnarray}
では、はさみうちの原理を証明してみる。
まず、\(f_2(x)-f_1(x)\)の極限を取ってみる。
\begin{eqnarray}
\lim_{x \to a}\left(f_2(x)-f_1(x)\right)=\lim_{x \to a}f_2(x)-\alpha\geqq0
\end{eqnarray}
次に\(f_3(x)-f_2(x)\)の極限を取ってみる。
\begin{eqnarray}
\lim_{x \to a}\left(f_3(x)-f_2(x)\right)=\alpha-\lim_{x \to a}f_2(x)\leqq0
\end{eqnarray}
以上の2つの極限値の積を考える。
\begin{eqnarray}
\left(\lim_{x \to a}f_2(x)-\alpha\right)\left(\alpha-\lim_{x \to a}f_2(x)\right)=-\left(\lim_{x \to a}f_2(x)-\alpha\right)^2
\end{eqnarray}
また、この極限値の積は\(0\)以上であることも分かる。
つまり、\(-\left(\lim_{x \to a}f_2(x)-\alpha\right)^2\geqq0\)を満たすためには、\(\lim_{x \to a}f(x)_2=\alpha\)である必要がある。
よって、はさみうちの原理の証明を終わる。
追い出しの原理
追い出しの原理は以下になる。
\begin{eqnarray}
f_1(x)&\leqq& f_2(x)\\
\\
\lim_{x \to a}f_1(x)&=&\pm\infty
\end{eqnarray}
以上のことを満たす時、以下を満たす。
\begin{eqnarray}
\lim_{x \to a}f_2(x)=\pm\infty
\end{eqnarray}
では、追い出しの原理についても証明してみる。
まず、\(f_2(x)-f_1(x)\geqq0\)の極限を取る。
\begin{eqnarray}
\lim_{x \to a}\left(f_2(x)-f_1(x)\right)=\lim_{x \to a}f_2(x)-\infty\geqq0\\
\\
\lim_{x \to a}f_2(x)\geqq\infty
\end{eqnarray}
\(\infty\)以上の値は\(\infty\)に他ならない。
よって、以下を満たす。
\begin{eqnarray}
\lim_{x \to a}f_2(x)=\infty
\end{eqnarray}
\(-\infty\)ついても同様である。
よって、追い出しの原理の証明を終わる。
まとめ
本記事では極限の考え方について説明した。
その内容を以下にまとめる。
- 極限とは任意の関数\(f(x)\)の変数\(x\)をある値\(a\)に限りなく近づけると極限値を取る場合がある。
\begin{eqnarray}
\lim_{x \to \pm a}f(x)=\begin{cases}
\pm\infty & 発散する\\
\\
\alpha & 収束する\\
\\
極限値は存在しない
\end{cases}
\end{eqnarray} - 極限値の定理としてはさみうちの原理と追い出しの原理がある。
極限値は関数を近似する時に用いることが多い。
かくいう微分も近似の一つである。
だが、その近似はとても精度が良いので様々なところで使われている。
演習問題
問1
以下の極限を求めよ。
\begin{eqnarray}
\lim_{x \to \infty}\frac{2x-1}{3x+2}
\end{eqnarray}
\lim_{x \to \infty}\frac{2x-1}{3x+2}&=&\lim_{x \to \infty}\frac{2-\frac{1}{x}}{3+\frac{2}{x}}\\
\\
&=&\frac{2}{3}
\end{eqnarray}
問2
以下の極限値になることを証明せよ。
\begin{eqnarray}
\lim_{\theta \to 0}\frac{\sin \theta}{\theta}=1
\end{eqnarray}
\lim_{\theta \to 0}\sin \theta=\theta
\end{eqnarray}
を証明する。
まず、中心を2次元平面上の原点\(O\)とした半径1の単位円を考える。(図)
単位円上の点を\(P(x,y)\)として、極座標表示で表すと\((x,y)\)は以下になる。
\begin{eqnarray}
x=\cos\theta\\
\\
y=\sin\theta
\end{eqnarray}
点\(P\)から\(x\)軸上に垂線を下ろして、\(x\)軸との交点を\(H\)とする。
この時、\(PH=\sin\theta\)である。
また、\((1,0)\)から単位円上に沿って点\(P\)までの円弧\(XP\)の長さは\(\theta\)である。
ここで、\(\theta→0\)の極限を取ると、円弧\(XP\)と線分\(PH\)の長さはほぼ等しくなることが分かる。
よって、以下の極限を満たす。
\begin{eqnarray}
\lim_{\theta \to 0}\sin\theta=\theta
\end{eqnarray}
よって、以下の極限を満たす。
\begin{eqnarray}
\lim_{\theta \to 0}\frac{\sin\theta}{\theta}&=&\frac{\theta}{\theta}\\
\\
&=&1
\end{eqnarray}
問3
以下の極限を求めよ。
\begin{eqnarray}
\lim_{a \to \infty}\int_{b}^{a}&&G\frac{mM}{r^2}dr\\
\\
&&G,m,M:定数
\end{eqnarray}
\begin{eqnarray}
\int_{b}^{a}G\frac{mM}{r^2}dr&=&-GmM\left[\frac{1}{r}\right]_b^a\\
\\
&=&-GmM\left(\frac{1}{a}-\frac{1}{b}\right)
\end{eqnarray}
この積分の結果から極限を計算する。
\begin{eqnarray}
\lim_{a \to \infty}-GmM\left(\frac{1}{a}-\frac{1}{b}\right)&=&\frac{GmM}{b}
\end{eqnarray}
この問題の意味することを説明する。
まず、\(G\frac{mM}{r^2}\)は重力の式である。
\(r\)は位置を表す。
また、計算した積分はある位置\(b\)から\(a\)まで物体を動かす時に必要なエネルギーを表す。
物体を動かす位置\(a\)を無限大に極限を取ったら、\(\frac{GmM}{b}\)という結果が得られた。
つまり、物体を遥か彼方にまで動かすためのエネルギーは無限大に大きなエネルギーではなく、\(\frac{GmM}{b}\)という決められたエネルギーで十分であることが分かる。
一見、遥か彼方に物体を動かそうとすると無限大のエネルギーが必要と思うかもしれないが、本当は最初の位置で決められたエネルギーだけを物体に与えれば良い。
但し、これは空気抵抗などの摩擦がない宇宙空間での話である。
物体を動かす時に摩擦が生じると、エネルギーロスが生じるので余分なエネルギーが必要になる。
問4
以下の極限値を求めよ。
\begin{eqnarray}
\lim_{h \to 0}\frac{\left(x+h\right)^n-x^n}{h}
\end{eqnarray}
\lim_{h \to 0}\frac{\left(x+h\right)^{n}-x^{n}}{h}&=&\lim_{h \to 0}\frac{\sum_{k=0}^{n}{}_nC_k\left(x^{n-k}h^{k}\right)-x^n}{h}\\
\\
&=&\lim_{h \to 0}\frac{\sum_{k=1}^n{}_nC_kx^{n-k}h^{k}}{h}\\
\\
&=&\lim_{h \to 0}\underbrace{\sum_{k=1}^n{}_nC_kx^{n-k}h^{k-1}}_{h^{k-1}はk>1の時h→0により0}\\
\\
&=&nx^{n-1}
\end{eqnarray}