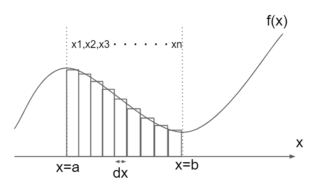
微分とは関数の変化具合を求める計算方法である。
図1のように直線の傾きを求める場合、任意の\(x\)から2点を選び、平均変化率を計算することで求めることができる。
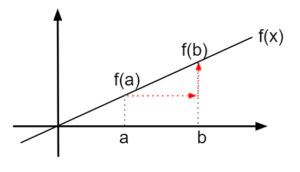 図1.関数f(x)の平均変化率(直線)
図1.関数f(x)の平均変化率(直線)だが、図2のように曲線の場合、正確な傾きを求めることができない。
なぜなら、平均変化率は\(a-b\)間の曲線の変化を表していないからである。
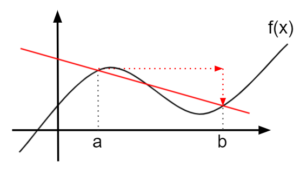 図2.関数f(x)の平均変化率(曲線)
図2.関数f(x)の平均変化率(曲線)この問題を解決する方法が微分である。
微分とは、微小間の平均変化率を計算することで、関数\(f(x)\)の傾きを全ての\(x\)について求めることができる。
平均変化率について
平均変化率とは傾き(直線)
平均変化率は関数の変化具合を表している。
図1から平均変化率は以下のように計算できる。
\begin{eqnarray}
平均変化率=\frac{f(b)-f(a)}{b-a}
\end{eqnarray}
関数\(f(x)\)は、\(x=a\)から\(x=b\)に変化するまでにどれくらい変化したかを表す。
特に、関数が直線の場合は、平均変化率は直線の傾きを表す。
曲線の場合の平均変化率の問題点
次に、関数が曲線の場合を考えてみる。
図2のように関数が曲線の場合、平均変化率を計算すると図2のようになる。
このとき、求めた平均変化率は\(x=a\)と\(x=b\)のみで決まる。
しかし、平均変化率は\(x=a\)から\(x=b\)まで関数がどのように変化しているかを表すことはできない。
これが、従来の平均変化率の問題点である。
a-b間を小さくすると正確な傾きを求められる
では、関数がどのように変化しているかを表すにはどうすればいいのか。
まずは、\(a-b\)間を小さくしてみる。
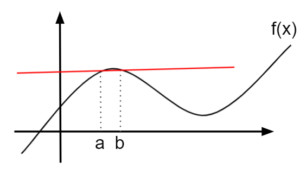 図3.図2よりa-b間を小さくした平均変化率
図3.図2よりa-b間を小さくした平均変化率すると、\(a-b\)間の関数の変化具合を図2より正確に表せている。(図3)
つまり、平均変化率を計算するとき、変化の幅を小さくすることで、正確な関数の変化を求めることができる。
微分とは、この変化の幅を微小な値にして平均変化率を求める計算である。
言い換えれば、変化の幅を極限\(0\)を取ることである。
微分について
a-b間を0に近づけることで直線とみなす
まずは、従来の平均変化率を書いてみる。
\begin{eqnarray}
平均変化率=\frac{f(b)-f(a)}{b-a}
\end{eqnarray}
ここで、\(x=b\)の表記方法を変える。
\(x=b\)は\(x=a\)からどれだけ変化しているかを表すために、\(b=a+dx\)と表す。
よって、平均変化率を書き換えると以下になる。
\begin{eqnarray}
平均変化率=\frac{f(a+dx)-f(a)}{dx}
\end{eqnarray}
次に微分の考え方について思い出す。
変化の幅を微小な値にして、平均変化率を計算することが微分である。
ここでの、変化の幅は\(dx\)である。
この\(dx\)の極限\(dx→0\)を取る。
すると、平均変化率は以下になる。
\begin{eqnarray}
平均変化率=\lim_{dx \to 0}\frac{f(a+dx)-f(a)}{dx}\tag{①}
\end{eqnarray}
式①の意味をグラフにして考えてみる。
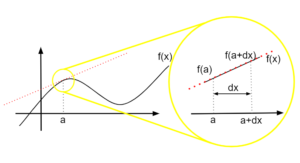 図4.x=aでの拡大図
図4.x=aでの拡大図求めた平均変化率は\(x=a\)から\(x=a+dx\)の幅で計算している。
また、変化の幅\(dx\)は極限を取って\(dx→0\)である。
すると、\(x=a\)から\(x=a+dx\)の範囲では、関数を直線とみなすことができる。
直線とみなした関数の傾きを、式①は表している。
つまり、式①は\(x=a\)での関数の傾きを近似的に表している。
任意のxで成り立つ
\(x=a\)での関数の傾きについて考えてみた。
だが、この計算は\(x=a\)だけではない。
関数が取ることができる全ての\(x\)において、計算することができる。
式①は全ての\(x\)の中での一つの計算に過ぎない。
つまり、式①を全ての\(x\)に対応させると、以下になる。
\begin{eqnarray}
平均変化率=\lim_{dx \to 0}\frac{f(x+dx)-f(x)}{dx}
\end{eqnarray}
微分の表記方法
関数\(f(x)\)の微分は\(f'(x),\frac{df(x)}{dx}\)と表す。
つまり、以下のようにかける。
\begin{eqnarray}
f'(x)=\frac{df(x)}{dx}=\lim_{dx \to 0}\frac{f(x+dx)-f(x)}{dx}
\end{eqnarray}