微積分は物体の運動を表すことができる。
図1はある物体の運動を\(v-t\)グラフで表している。
このとき、時間\(t=t_0\)から\(t=t_1\)までの間に物体が進んだ距離は、斜線部の面積と等しい。
つまり、以下のように積分で表すことができる。
\begin{eqnarray}
進んだ距離=\int_{t_0}^{t_1}v(t)dt
\end{eqnarray}
また、物体の加速度は関数\(v(t)\)の傾きである。
つまり、速度\(v(t)\)を時間\(t\)で1階微分することで表すことができる。
\begin{eqnarray}
加速度=\frac{v(t)}{dt}
\end{eqnarray}
このように、微積分を用いて物体の運動を表すことができる。
微積分について
本章では、微積分とはなんだったのかおさらいしてみる。
微分 関数の変化を表す
微分とは関数の変化を表す。
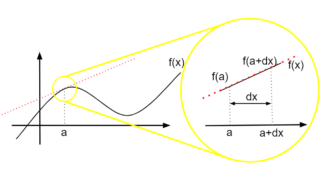
ある関数\(f(x)\)の微分は以下で定義される。
\begin{eqnarray}
\frac{f(x)}{dx}=\lim_{dx \to 0}\frac{f(x+dx)-f(x)}{dx}\tag{1.1}
\end{eqnarray}
式1は、関数\(f(x)\)における\(x\)から\(x+dx\)までの平均変化率を表している。
また、\(dx\)は微小であることにも注意すると、関数\(f(x)\)が\(x\)の瞬間においてどれだけ変化しているかを式1は表している。
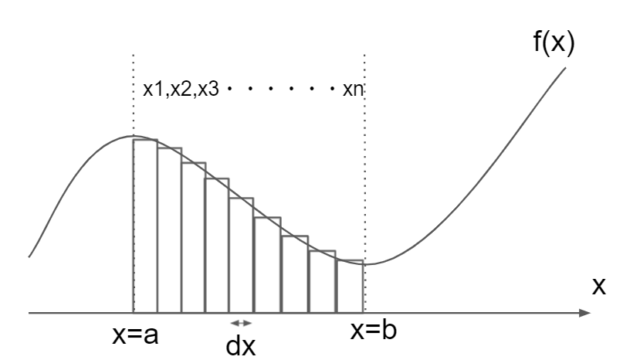
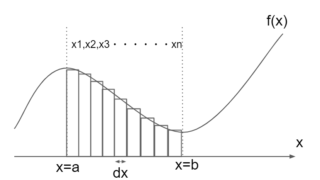
積分 関数からできる面積を表す
積分をグラフで表すと、図2における斜線部の面積を表す。
斜線部の範囲を幅\(dx\)の長方形に分ける。
このとき、\(dx\)は微小な値を取る。
すると、全ての長方形の面積の総和は斜線部の面積と等しくなる。
\begin{eqnarray}
長方形の面積の総和=斜線部の面積
\end{eqnarray}
よって、長方形の面積の総和を計算することで、斜線部の面積を求めることができる。
斜線部の面積を表すと以下のように表せる。
\begin{eqnarray}
斜線部の面積=\int_{b}^{a}f(x)dx
\end{eqnarray}
微積分を物体の運動に応用
本章では、実際に速度、加速度、物体の位置の3つの値を微積分を用いて表してみる。
速度\(v=\frac{dx}{dt}\)
速度\(v(t)\)を物体の位置\(x(t)\)で表すと、以下になる。
\begin{eqnarray}
v(t)=\frac{dx(t)}{dt}\tag{2.1}
\end{eqnarray}
なぜ、物体の速度\(v(t)\)を式2.1のように表せるのか考えてみる。
ある物体の位置\(x\)の時間変化をグラフにして見てみると、図2.1のようになる。
位置\(x\)を大きく分けて\(Ⅰ、Ⅱ、Ⅲ\)とする。
\(Ⅰ\)では、\(x\)があまり大きくならない。
つまり、物体の進みが遅いことを表している。
\(Ⅱ\)では、\(x\)が急激に大きくなっている。
つまり、物体の進みが速いことを表している。
\(Ⅲ\)では、再び\(x\)があまり大きくならない。
つまり、物体の進みが遅いことを表している。
言い換えると、\(Ⅰ、Ⅲ\)では物体の速度は小さいが、\(Ⅱ\)では速度は大きいことを表している。
そして、速度の大きさは関数\(x(t)\)の傾きによることが考えられる。
ここで、速度の求め方を思い出す。
ある時間\(t=t_1\)から\(t=t_2\)まで進んだときの物体の速度は、以下である。
\begin{eqnarray}
物体の速度=\frac{x(t_2)-x(t_1)}{t_2-t_1}\tag{2.2}
\end{eqnarray}
\(t_2\)を\(t_1\)から微小な時間\(dt\)だけ経過した時間\(t_2=t_1+dt\)とする。
このとき、\(dt→0\)という極限を取っている。
すると、式2.2は以下になる。
\begin{eqnarray}
物体の速度=\lim_{dt \to 0}\frac{x(t_1+dt)-x(t_1)}{dt}\tag{2.3}
\end{eqnarray}
式2.3は\(x(t=t_1)\)の微分である。
さらに、\(t_1\)はどの時間\(t\)を取っても良い。
よって、物体の速度\(v(t)\)は以下のように表せる。
\begin{eqnarray}
v(t)&=&\lim_{dt \to 0}\frac{x(t+dt)-x(t)}{dx}\\
\\
&=&\frac{dx(t)}{dt}\tag{2.4}
\end{eqnarray}
式2.4は、物体がある時間\(t\)の一瞬での速度を表している。
加速度\(\alpha=\frac{dv}{dt}\)
加速度\(\alpha(t)\)を速度\(v(t)\)で表すと、以下になる。
\begin{eqnarray}
\alpha(t)=\frac{dv(t)}{dt}\tag{2.5}
\end{eqnarray}
なぜ、物体の加速度\(\alpha(t)\)を式2.5のように表せるのか考えてみる。
ある物体の速度\(v\)の時間変化をグラフにして見てみると、図2.2のようになる。
図2.2は図2.1の\(x-t\)グラフにしたがって運動をする物体を元にした\(v-t\)グラフである。
速度\(v\)を大きく分けて\(Ⅰ、Ⅱ、Ⅲ\)とする。
ここで、\(Ⅰ、Ⅱ、Ⅲ\)へ移行するときの速度がどのように変化をしているかを見てみる。
\(Ⅰ→Ⅱ\)では、速度が急激に大きくなっている。
つまり、速度は加速していることがわかる。
\(Ⅱ→Ⅲ\)では、速度が急激に小さくなっていることがわかる。
つまり、速度は減速していることがわかる。
言い換えると、\(Ⅰ→Ⅱ\)では加速度は正の値を取り、\(Ⅱ→Ⅲ\)では加速度は負の値を取ることがわかる。
\begin{eqnarray}
Ⅰ→Ⅱ&:&加速度\alpha>0\\
\\
Ⅱ→Ⅲ&:&加速度\alpha<0
\end{eqnarray}
ここで、加速度の求め方を思い出す。
ある時間\(t=t_1\)から\(t=t_2\)まで加速したときの物体の加速度は、以下である。
\begin{eqnarray}
物体の加速度=\frac{v(t_2)-v(t_1)}{t_2-t_1}\tag{2.6}
\end{eqnarray}
\(t_2\)を\(t_1\)から微小な時間\(dt\)だけ経過した時間\(t_2=t_1+dt\)とする。
このとき、\(dt→0\)という極限を取っている。
すると、式2.6は以下になる。
\begin{eqnarray}
物体の加速度=\lim_{dt \to 0}\frac{v(t_1+dt)-v(t_1)}{dt}\tag{2.7}
\end{eqnarray}
式2.7は\(v(t=t_1)\)の微分である。
さらに、\(t_1\)はどの時間\(t\)を取っても良い。
よって、物体の加速度\(\alpha(t)\)は以下のように表せる。
\begin{eqnarray}
\alpha(t)&=&\lim_{dt \to 0}\frac{v(t+dt)-v(t)}{dx}\\
\\
&=&\frac{dv(t)}{dt}\tag{2.8}
\end{eqnarray}
式2.8は、物体がある時間\(t\)の一瞬での加速度を表している。
また、速度\(v(t)\)は位置\(x\)の1階微分であった。(式2.4)
よって、加速度\(\alpha(t)\)は位置\(x(t)\)の2階微分である。
以下のように表すこともできる。
\begin{eqnarray}
\alpha(t)=\frac{d^2x(t)}{dt^2}
\end{eqnarray}
物体の進んだ距離を積分で表す
これまで、物体の位置\(x\)、速度\(v\)、加速度\(\alpha\)の関係を微分で表してきた。
だが、微分の逆の計算方法は積分である。
つまり、\(x,v,\alpha\)は積分でも表すことができる。
図2.4は物体の速度\(v\)の時間変化を表したグラフである。
このグラフから、物体の位置\(x\)を積分を使って表してみる。
時間\(t\)の間に物体が進んだ距離を表すと以下になる。
\begin{eqnarray}
進んだ距離=vt\tag{2.9}
\end{eqnarray}
ここで、速度が一定(等速度運動)であれば時間\(t\)によらず式2.9で計算できる。
しかし、図2.4のように速度が時間によって変化する場合は、式2.9では物体の進んだ距離を求めることができない。
そこで、微小な時間\(dt\)の間に物体が進んだ距離を考えてみる。
微小な時間\(dt\)の間に一瞬で進んだ距離は以下のように表せる。
\begin{eqnarray}
一瞬で進んだ距離=v(t)dt\tag{2.10}
\end{eqnarray}
式2.10を図2.4においてどのように表されているか。
\(dt\)は微小なので、一瞬の間は\(v(t)\)は一定であるとみなす。
すると式2.10は、幅\(dt\)の長方形の面積を表す。(図2.5)
この\(dt\)に進んだ距離を長方形の面積として全ての\(t\)について求めて総和を計算すると、全体の物体の進んだ距離を計算することができる。
この考え方は積分と同じである。
よって、\(t=t_0\)から\(t=t_1\)の間に物体が進んだ距離は以下になる。
\begin{eqnarray}
物体の進んだ距離=\int_{t_0}^{t_1}v(t)dt\tag{2.11}
\end{eqnarray}
また、物体の進んだ距離を\(x(t)\)を用いて計算すると、以下になる。
\begin{eqnarray}
物体の進んだ距離=x(t_1)-x(t_0)\tag{2.12}
\end{eqnarray}
式2.11、2.12より、\(x(t)\)と\(v(t)\)の関係を積分で表すと以下になる。
\begin{eqnarray}
\int_{t_0}^{t_1}v(t)dt=x(t_1)-x(t_0)
\end{eqnarray}