はじめに
本記事ではガウス関数の積分について紹介する。
まず、ガウス関数とは以下のような関数である。
\begin{eqnarray}
f(x)=A\mathrm{e}^{-\alpha x^2}\\
\\
A,\alpha>0:定数
\end{eqnarray}
このガウス関数は図1.1のような関数である。
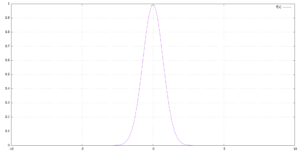 図1.1 ガウス関数(α=1)
図1.1 ガウス関数(α=1)主にこのガウス関数は以下のような積分範囲での積分を考えることが多い。
\begin{eqnarray}
I(x)=\int_{-\infty}^{\infty}A\mathrm{e}^{-\alpha x^2}dx
\end{eqnarray}
本記事ではこのガウス関数の積分を極座標表示を用いて解いていく。
ガウス関数の積分の意味
最初にガウス関数の積分を計算していく前に、ガウス関数の積分の意味を考えていく。
図1.1でも見たように、ガウス関数は以下のような関数である。
 ガウス関数(α=1)
ガウス関数(α=1)このガウス関数の特徴としては、\(x→-\infty,\infty\)の極限を取ったときに\(0\)に収束するということである。
すると、ガウス関数と横軸(ここではx軸)の間の面積は発散せず収束する、つまりある定数になることが分かる。
ガウス関数の積分の意味とは、このガウス関数と横軸の間の面積を求めることである。

ガウス関数の積分の解法
デカルト表示→極座標表示
では、実際にガウス関数の積分を計算していく。
まず、ガウス関数の積分を以下のように\(I\)と置く。
\begin{eqnarray}
I=\int_{-\infty}^{\infty}A\mathrm{e}^{-\alpha x^2}dx
\end{eqnarray}
ここでの積分の変数は\(x\)を用いている。
だが、変数は任意である。(どんな変数を用いても良い。)
そこで、変数を\(y\)と置いても積分の値は変わらない。
つまり、以下のことが言える。
\begin{eqnarray}
I=\int_{-\infty}^{\infty}A\mathrm{e}^{-\alpha y^2}dy
\end{eqnarray}
よって、\(I^2\)は以下の様になる。
\begin{eqnarray}
I^2=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}A^2\mathrm{e}^{-\alpha (x^2+y^2)}dxdy
\end{eqnarray}
ここで、デカルト座標から極座標へと変数を変換させる。
\(x,y\)と\(r,\theta\)の関係は以下である。
\begin{eqnarray}
x&=&r\cos\theta\\
y&=&r\sin\theta
\end{eqnarray}
これらの変数変換を使って、積分\(I^2\)を書き換えると以下のようになる。
\begin{eqnarray}
I^2=\int_{0}^{\infty}\int_{0}^{2\pi}A^2\mathrm{e}^{-\alpha r^2}rdrd\theta\\
\\
x^2+y^2=r^2\\
\\
dxdy=rdrd\theta
\end{eqnarray}
この積分を\(r\)と\(\theta\)について計算していく。
まず、\(\theta\)について計算する。
\(\theta\)は積分する関数の中に含まれていないので、定数として積分を実行すると以下のようになる。
\begin{eqnarray}
I^2&=&A^2\int_{0}^{2\pi}d\theta\int_{0}^{\infty}\mathrm{e}^{-\alpha r^2}rdr\\
\\
&=&A^{2}2\pi\underbrace{\int_{0}^{\infty}\mathrm{e}^{-\alpha r^2}rdr}_{g}
\end{eqnarray}
次に\(r\)について積分をする。
\(r\)の積分部分を以下のように定数を変えると積分を実行できる。
\begin{eqnarray}
g&=&\int_{0}^{\infty}\underbrace{\frac{1}{-2\alpha}\left(-2\alpha\right)}_{=1}r\mathrm{e}^{-\alpha r^2}dr\\
\\
&=&\frac{1}{-2\alpha}\left[\mathrm{e}^{-\alpha r^2}\right]_{0}^{\infty}\\
\\
&=&\frac{1}{2\alpha}
\end{eqnarray}
よって、\(I^2\)は以下のようになる。
\begin{eqnarray}
I^2&=&A^22\pi\frac{1}{2\alpha}\\
\\
&=&A^2\frac{\pi}{\alpha}
\end{eqnarray}
よって、求めたいガウス関数の積分\(I\)は以下のようになる。
\begin{eqnarray}
I=A\sqrt{\frac{\pi}{\alpha}}
\end{eqnarray}

指数関数の肩が二次関数の場合は平方完成してから置換積分
次にガウス関数が以下の場合の積分を考える。
\begin{eqnarray}
J=\int_{-\infty}^{\infty}e^{-\alpha x^2+\beta x+\gamma}
\end{eqnarray}
この場合のように、指数関数の肩が二次式になっている場合がある。
この場合は二次式を平方完成して変数の2乗と定数の和に分ける必要がある。
実際に平方完成してみると指数関数の肩は以下になる。
\begin{eqnarray}
-\alpha x^2+\beta x+\gamma=-\alpha\left(x+\frac{\beta}{2\alpha}\right)^2+\frac{\beta^2}{4\alpha}+\gamma
\end{eqnarray}
よって、積分\(J\)は以下になる。
\begin{eqnarray}
J=\int_{-\infty}^{\infty}e^{-\alpha\left(x+\frac{\beta}{2\alpha}\right)^2+\frac{\beta^2}{4\alpha}+\gamma}dx\\
\\
=e^{\frac{\beta^2}{4\alpha}+\gamma}\int_{-\infty}^{\infty}e^{-\alpha\left(x+\frac{\beta}{2\alpha}\right)^2}dx
\end{eqnarray}
ここで、\(x’=x+\frac{\beta}{2\alpha}\)と置換をする。
この時、\(dx’=dx\)である。
よって、積分\(J\)は以下になる。
\begin{eqnarray}
J&=&e^{\frac{\beta^2}{4\alpha}+\gamma}\underbrace{\int_{-\infty}^{\infty}e^{-\alpha x’^2}dx’}_{=I}\\
\\
&=&e^{\frac{\beta^2}{4\alpha}+\gamma}\sqrt{\frac{\pi}{\alpha}}
\end{eqnarray}

発展:ガウス関数と\(\cos x\)の積の積分
最後の積分は少し難しい。
なぜなら、オイラーの公式を知らなければこの積分は解けないからである。
考える積分は以下である。
\begin{eqnarray}
K=\int_{-\infty}^{\infty}\cos xe^{-\alpha x^2}dx
\end{eqnarray}
ここで、以下の積分を考える。
\begin{eqnarray}
\int_{-\infty}^{\infty}\underbrace{\sin x}_{奇関数}\underbrace{e^{-\alpha x^2}}_{偶関数}dx
\end{eqnarray}
この積分は奇関数\(\sin x\)と偶関数\(e^{-\alpha x^2}\)の積なので、奇関数の積分となり値は\(0\)である。
よって、積分\(K\)に以上の積分を加えても問題ない。
すると、積分\(K\)は以下のように書き換えることができる。
\begin{eqnarray}
K&=&\int_{-\infty}^{\infty}\cos xe^{-\alpha x^2}dx+i\int_{-\infty}^{\infty}\sin xe^{-\alpha x^2}dx\\
\\
&=&\int_{-\infty}^{\infty}\underbrace{\left(\cos x+i\sin x\right)}_{e^{ix}}e^{-\alpha x^2}dx\\
\\
&=&\int_{-\infty}^{\infty}e^{-\alpha x^2+ix}dx
\end{eqnarray}
ここまでくれば、前節で行った平方完成を指数関数の肩について実行すれば良い。
よって、積分\(K\)は以下の値を取る。
\begin{eqnarray}
K=e^{-\frac{1}{4\alpha}}\sqrt{\frac{\pi}{\alpha}}
\end{eqnarray}
まとめ
本記事ではガウス関数の積分について説明してきた。
その内容をまとめる。
- ガウス関数の積分は横軸とガウス関数の間の面積であり、この面積は収束する。
- 直交座標から極座標へと変換して積分を実行する。
- 平方完成やオイラーの公式を使用して\(e^{-\alpha x^2}\)の形に変形して積分を実行する。
ガウス関数は高校ではあまり出てこないかもしれないが、大学物理では沢山見かけることがある。
ガウス関数の積分の意味や計算を高校の内に理解しておけば、大学でも役に立つだろう。