問題
問1
以下の方程式とxの範囲においてyの最小値と最大値を求めよ。
\begin{eqnarray}
y=x^2+2x\\
\left(-4\leq x\leq1\right)
\end{eqnarray}
問2
以下の方程式とxの範囲においてyの最小値と最大値を求めよ。
\begin{eqnarray}
y=-x^2-x+2\\
\left(-2< x <0\right)\end{eqnarray}
問3
以下の方程式とxの範囲においてyの最小値と最大値を求めよ。
\begin{eqnarray}
y=2x^2-4ax-a\\
\left(0\leq x\leq2\right)
\end{eqnarray}
問4
以下の方程式の最小値をkとする。
$$y=x^2-2mx+m$$
この時、kをmで表し、kの最大値を求めよ。
問5
以下の方程式とxの範囲においてyの最小値を求めよ。
\begin{eqnarray}
y=x^2+6x+5\\
\left(a\leq x\leq a+2\right)
\end{eqnarray}
問6
以下の方程式がある。
$$2x+y=1$$
この時、以下の値の最小値を求めよ。
$$x^2+y^2$$
解答
問1の解答 xの範囲と頂点の位置を考える
最初に方程式を平方完成する。
【平方完成の方法はこちら】
方程式を平方完成すると以下になる。
$$y=\left(x+1\right)^2-1$$
グラフは図1.1の様に描ける。
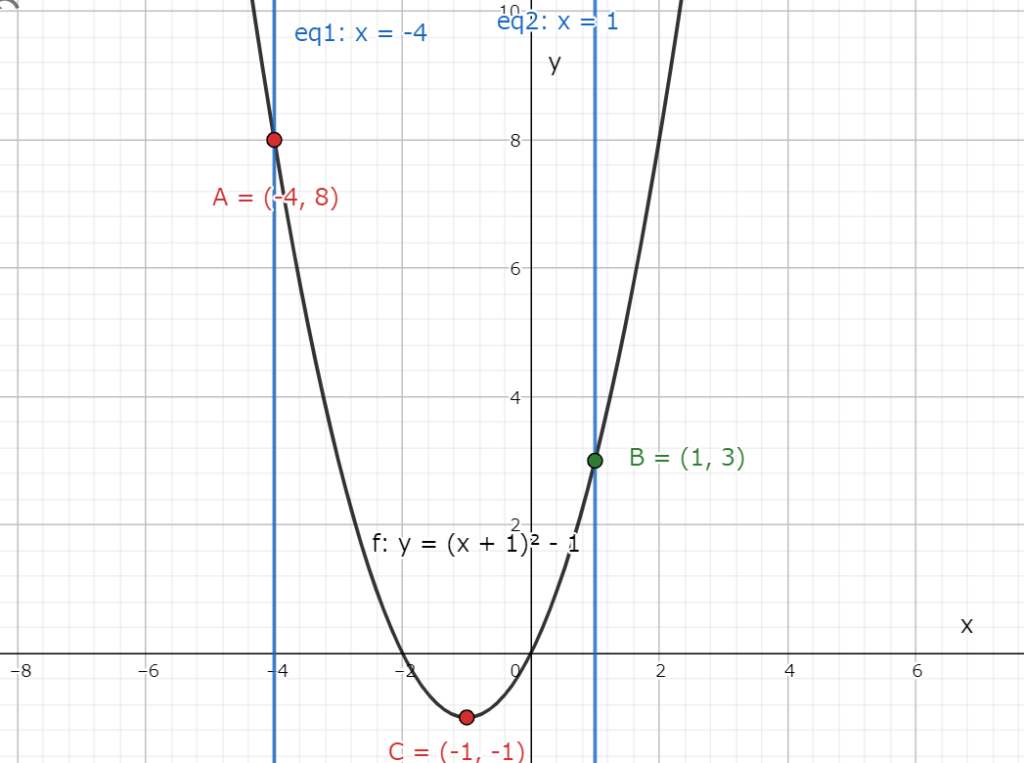 図1.1 放物線とxの範囲を表したグラフ
図1.1 放物線とxの範囲を表したグラフよって、最小値は放物線の頂点で取る。
また、最大値はxの範囲の端であるx=-4の時の値になる。
よって、グラフとxの範囲から最大値と最小値は以下になる。
\begin{eqnarray}
最大値&:&y(x=-1)=8\\
最小値&:&y(x=-4)-1
\end{eqnarray}
問2の解答 xの範囲に等号が付いていないことに注意
最初に方程式を平方完成する。
【平方完成の方法はこちら】
方程式を平方完成すると以下の様になる。
$$y=-\left(x+\frac{1}{2}\right)^2+\frac{9}{4}$$
グラフは図2.1の様に描ける。
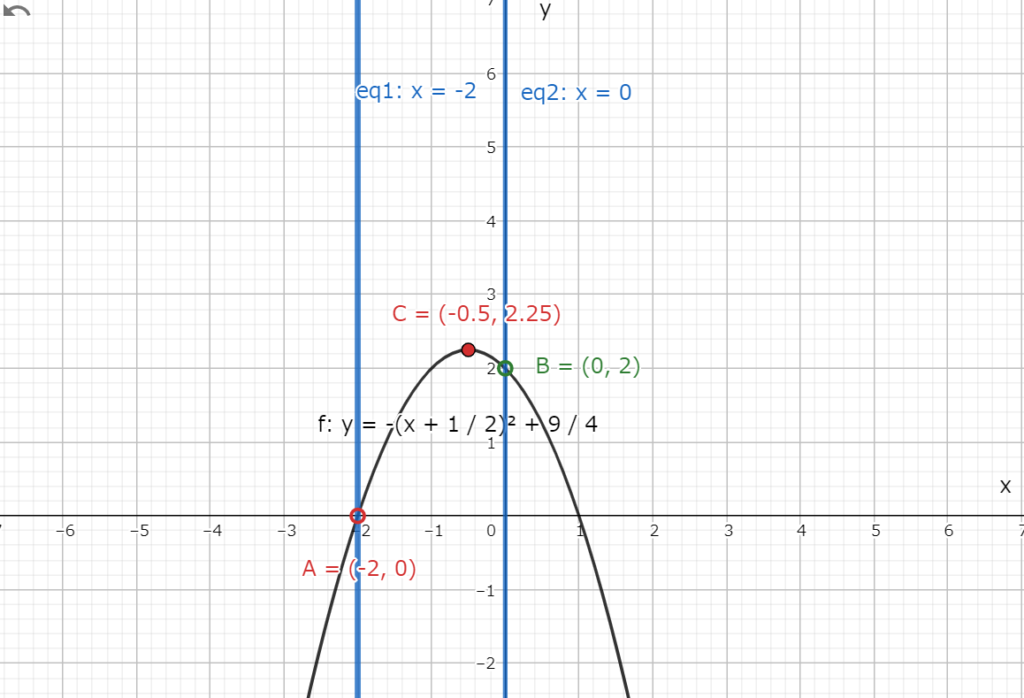 図2.1 放物線とxの範囲を表したグラフ
図2.1 放物線とxの範囲を表したグラフここで、最大値は頂点で取ることが分かる。
一方で最小値について考える。
xの範囲は等号が入っていない不等号である。
よって、xは-2の値を取らない。
【不等式についてはこちら】
よって、この時の最小値は存在しない。
最大値は以下になる。
$$最大値:y(x=-\frac{1}{2})=\frac{4}{9}$$
問3の解答 aによる放物線の変化に注意しながら場合分け
最初に方程式を文字aが入ったまま平方完成をする。
方程式を平方完成すると以下になる。
$$y=2\left(x-a\right)^2-2a^2-a$$
この方程式が意味することは放物線の頂点がaの値によって変わるということである。
更にxの範囲は決まっている。
よって、aの値によって放物線の最大値と最小値が変わる。
よって、aの値による場合分けをする。
- $$a<0の場合$$
放物線の頂点の位置は図3.1の様にxの範囲の負の方向にずれている(a=0.5の場合のグラフ)。
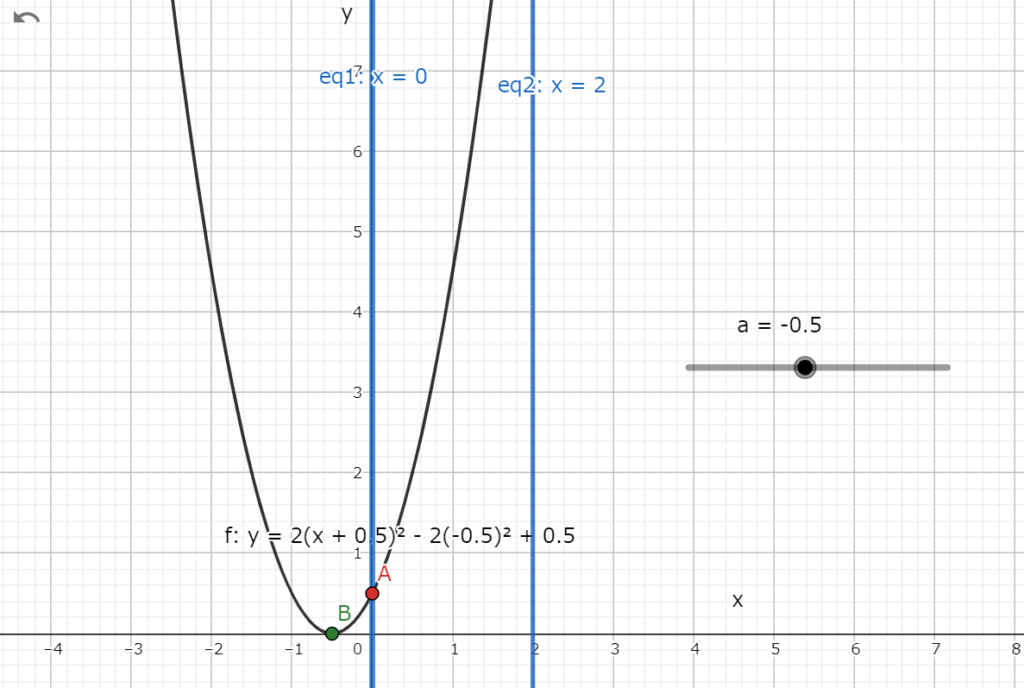 図3.1 放物線がxの範囲から左にずれているグラフ(a=0.5の場合)
図3.1 放物線がxの範囲から左にずれているグラフ(a=0.5の場合)よって、最小値はx=0の時に取る。
よって、最小値は以下となる。
$$y(x=0)=-a$$
- $$0\leq a\leq2の場合$$
この場合は図3.2の様に頂点がxの範囲の中にある(a=0.6の場合のグラフ)。
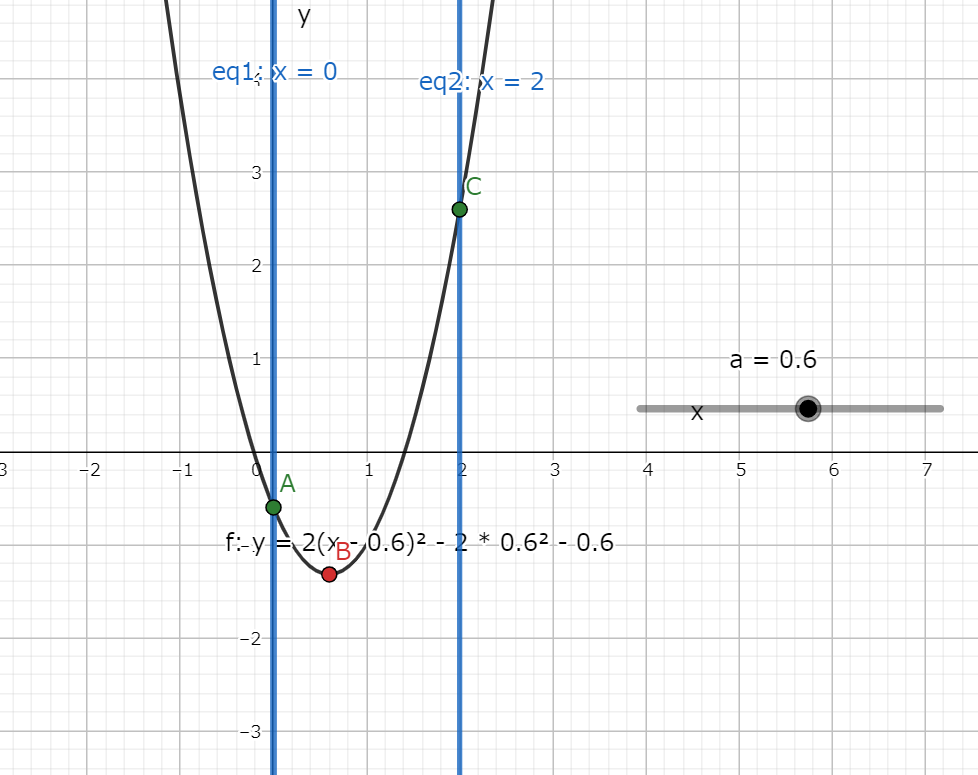 図3.2 放物線がxの範囲の中に入っているグラフ(a=0.6の場合)
図3.2 放物線がxの範囲の中に入っているグラフ(a=0.6の場合)よって、最小値は頂点で取る。
よって、最小値は以下になる。
$$y=(x=a)=-2a^2-a$$
- $$2< aの場合$$
放物線の頂点は図3.3の様にxの範囲の右にずれている(a=2.6)。
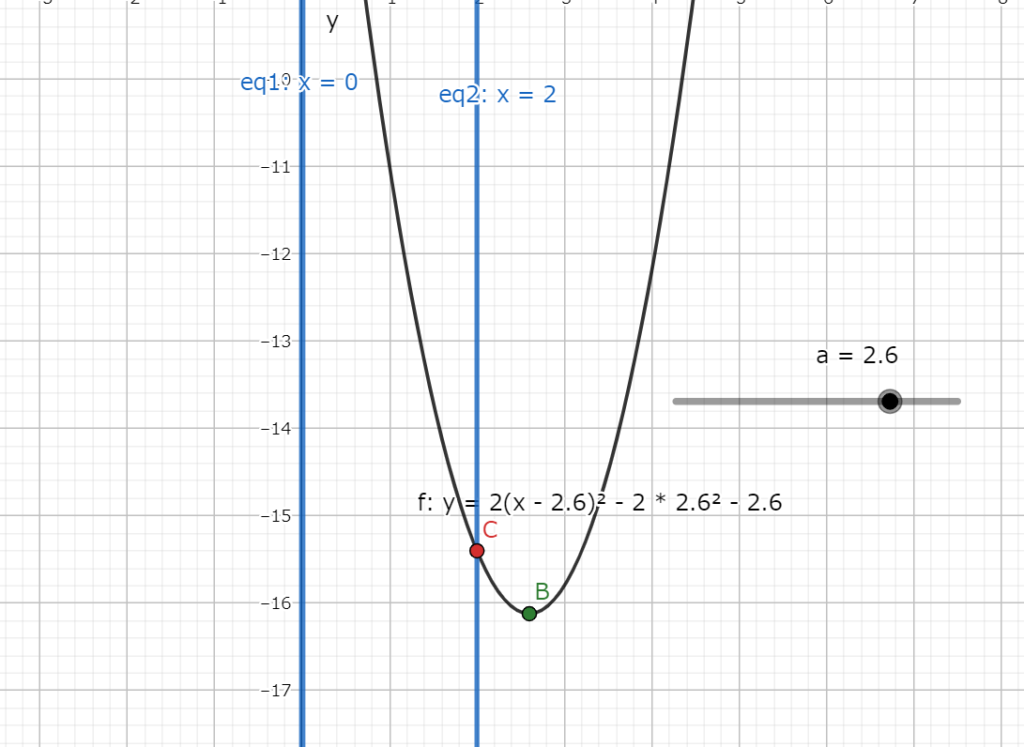 図3.3 放物線がxの範囲から右にずれているグラフ(a=2.6の場合)
図3.3 放物線がxの範囲から右にずれているグラフ(a=2.6の場合)よって、最小値はx=2の時に取る。
よって、最小値は以下になる。
$$y(x=2)=8-9a$$
- $$1\leq aの場合$$
放物線の頂点がxの範囲の真ん中であるx=1の直線の左側にあるので、最大値はx=2の時に取る。
よって、最大値は以下になる。
$$y(x=2)=8-9a$$
- $$a\geq 1の場合$$
放物線の頂点がxの範囲の真ん中であるx=1の直線の右側にあるので、最大値はx=0の時に取る。
よって、最大値は以下になる。
$$y(x=0)=-a$$
問4の解答 kとmの新しい関数を考える
最初に文字が入ったまま平方完成をする。
方程式を平方完成すると以下になる。
$$y=\left(x-m\right)^2-m^2+m$$
グラフは図4.1の黒のグラフの様に描ける。
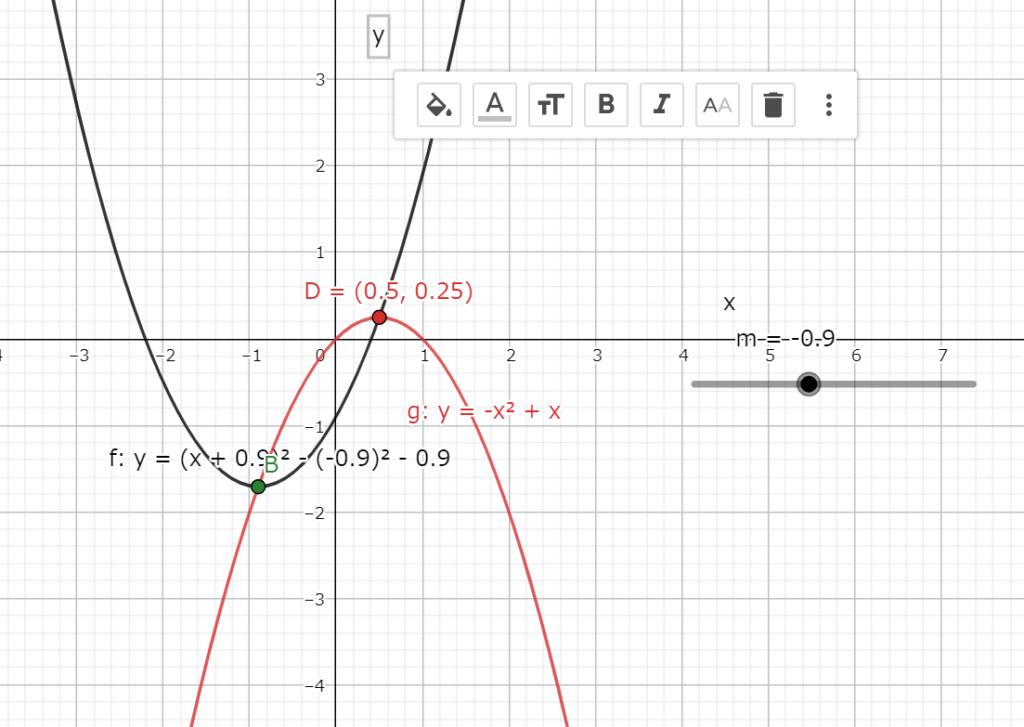 図4.1 放物線のグラフとその最小値kが取りうるグラフ
図4.1 放物線のグラフとその最小値kが取りうるグラフグラフから方程式の最小値はmの値によらず頂点の位置で取ることが分かる。
よって、kをmで表すと以下になる。
$$k=-m^2+m$$
次にkの最大値を求める。
これはkをmの関数で表したのでkをmで平方完成した方程式から考える。
kの方程式を平方完成すると以下になる。
$$k=-\left(m-\frac{1}{2}\right)^2+\frac{1}{4}$$
グラフは図4.1の赤のグラフの様に描ける。
グラフからkの最大値は頂点で取ることが分かる。
よって、kの最大値は以下になる。
$$k(m=\frac{1}{2})=\frac{1}{4}$$
問5の解答 aによるxの範囲の変化に注意しながら場合分け
最初に平方完成をする。
【平方完成の方法はこちら】
方程式を平方完成すると以下になる。
$$y=\left(x+3\right)^2-4$$
この時、xの範囲はaの値によって変化する。
よって、yの最小値は放物線の頂点がxの範囲の中にある場合と範囲外にある場合で場合分けをする。
- $$a<5(a+2<-3)の場合$$
放物線の頂点は図5.1の様にxの範囲の右側にあるので(a=-5.6)、最小値はx=a+2の時に取る。
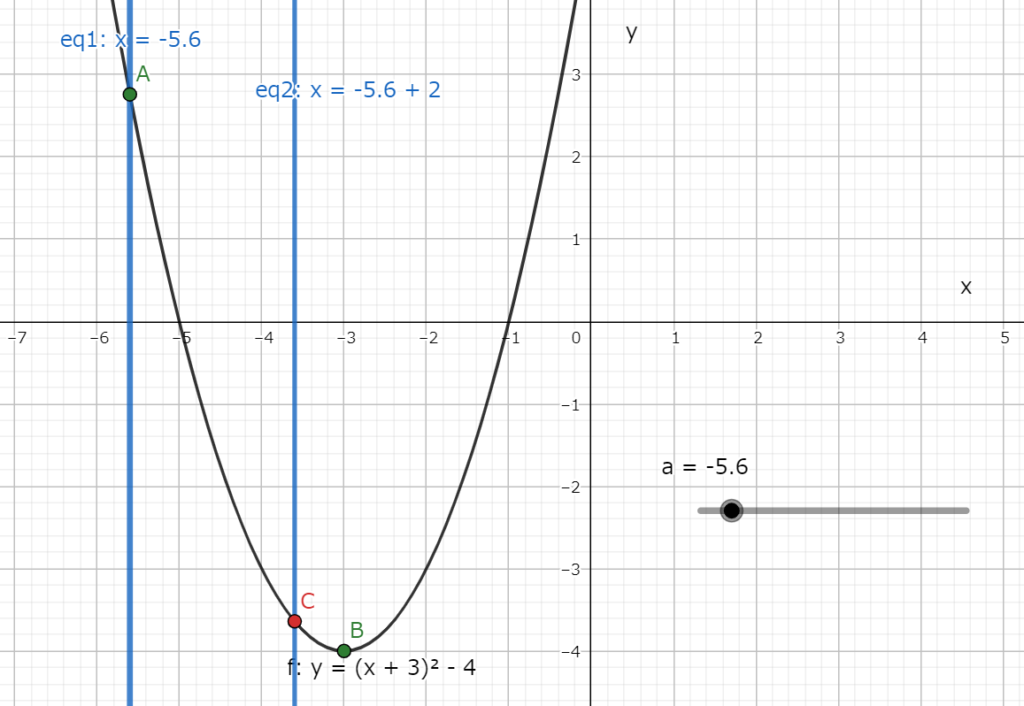 図5.1 放物線の頂点がxの範囲の右側にあるグラフ(a=-5.6の場合)
図5.1 放物線の頂点がxの範囲の右側にあるグラフ(a=-5.6の場合)よって、最小値は以下になる。
$$y(x=a+2)=a^2+10a+21$$
- $$-5\leq a\leq-3(a+2\geq-3かつa\leq-3)の場合$$
放物線の頂点は図5.2の様にxの範囲内にあるので、最小値は頂点の時に取る。
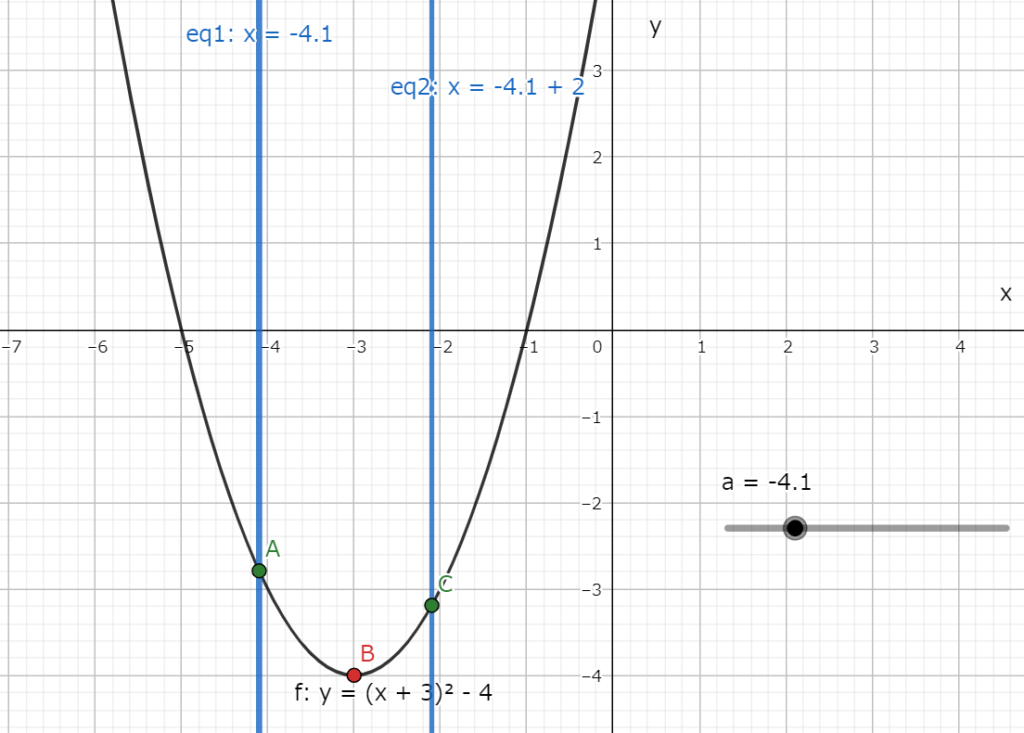 図5.2 放物線の頂点がxの範囲の中にあるグラフ(a=-4.1の場合)
図5.2 放物線の頂点がxの範囲の中にあるグラフ(a=-4.1の場合)よって、最小値は以下になる。
$$y(x=-3)=-4$$
- $$a>-3の場合$$
放物線の頂点は図5.3の様にxの範囲の左側にあるので、最小値はx=aの時に取る。
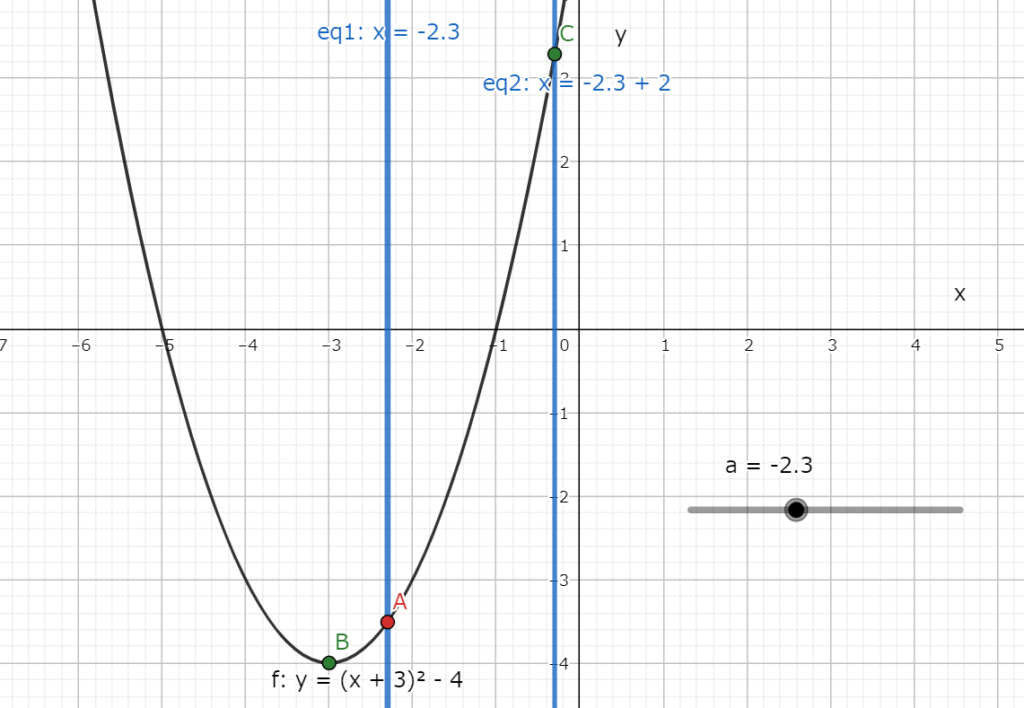 図5.3 放物線の頂点がxの範囲の左側にあるグラフ(a=-2.3の場合)
図5.3 放物線の頂点がxの範囲の左側にあるグラフ(a=-2.3の場合)よって、最長値は以下になる。
$$y(x=a)=a^2+6a+5$$
問6の解答 xとyの関係式を新しい関数zとおいて考える
最初にx^2+y^2をzと置く。
つまり、zは以下となる。
$$z=x^2+y^2\tag{式6.1}$$
そして、zの最小値を求めることにする。
ここで、zをxのみの関数にしたい。
なので、xとyの関係式を使う。
xとyの関係式をyの式に変形すると以下になる。
$$y=-2x+1\tag{式6.2}$$
次に式6.2を式6.1に代入して平方完成すると以下になる。
$$z=5\left(x-\frac{1}{5}\right)^2+\frac{1}{5}$$
グラフは図6.1の様に描ける。
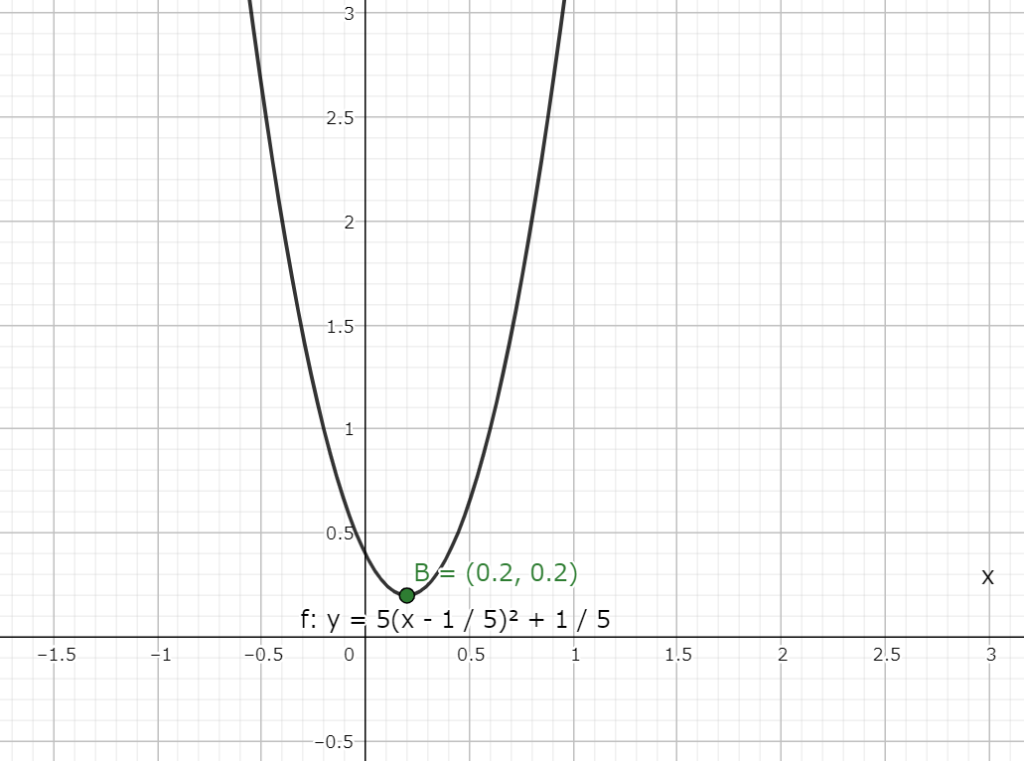 図6.1 zの放物線のグラフ
図6.1 zの放物線のグラフよって、zの最小値は頂点で取ることが分かる。
よって、zの最小値は以下になる。
$$z(x=\frac{2}{5},y=\frac{1}{5})=\frac{1}{5}$$
問6の解答は以上になるが、問6をイメージしやすく考えてみる。
まず、式6.1を図に表すとどうなるだろうか。
x軸、y軸、z軸を以下の図の様に決めると式6.1は図6.2のグラフの様に空間的に描ける。
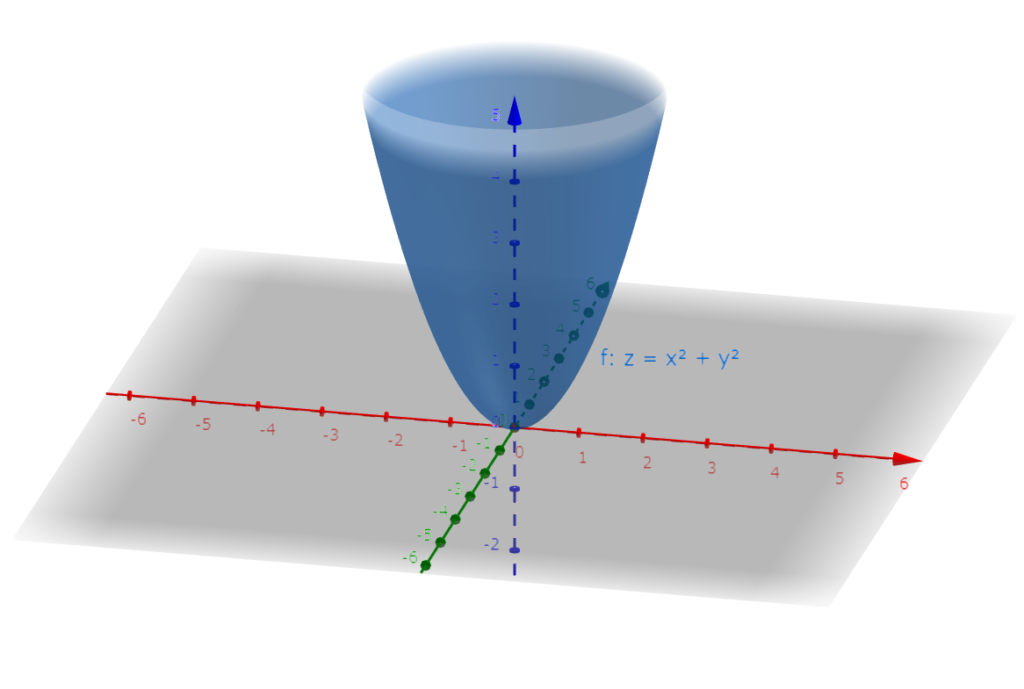 図6.2 式6.1を3次元で表したグラフ
図6.2 式6.1を3次元で表したグラフ更に、xとyの関係式である式6.2を図6.2に書き加えると図6.3のような赤色の平面の部分になる。
つまり、問6の問題は式6.1のグラフを式6.2の平面で切り取った時の最小値を求める問題なのである。
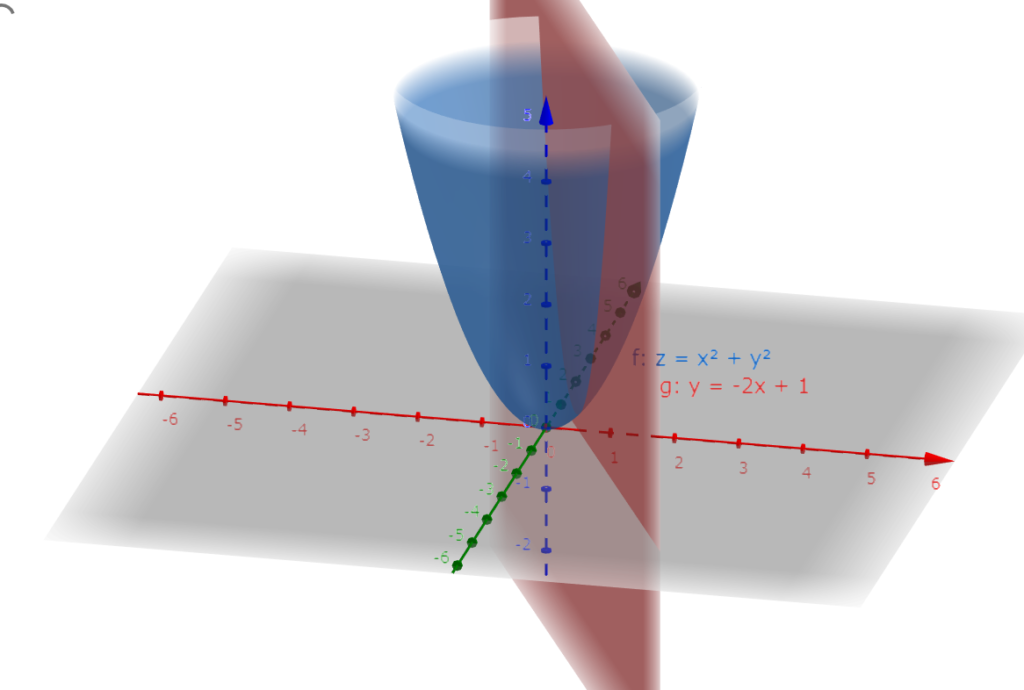 図6.3 式6.1のグラフに式6.2の平面を描いたグラフ
図6.3 式6.1のグラフに式6.2の平面を描いたグラフ図6.4は図6.3の式6.2の平面と垂直の方向から見たグラフである。
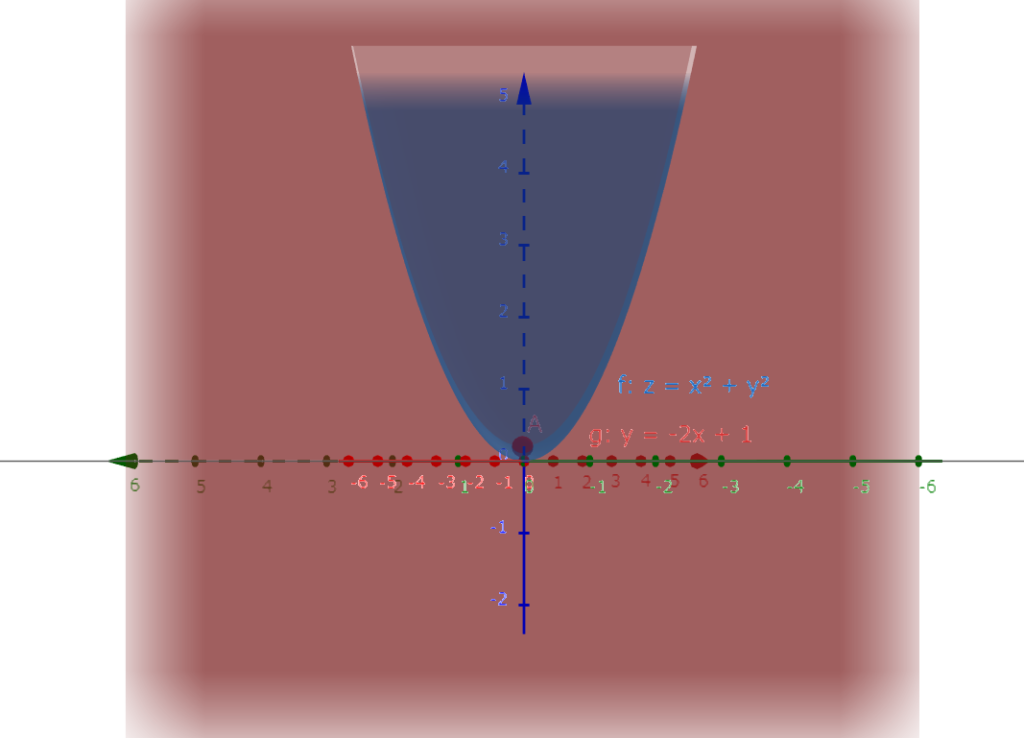 図6.4 図6.3の式6.2の平面に垂直な方向から見たグラフ
図6.4 図6.3の式6.2の平面に垂直な方向から見たグラフ図6.1の放物線のグラフと同じことが分かる。
このように問6はx,yの2つの変数からなるzの方程式を解く問題なのである。
(他の問題はxの1つの変数からなるyの方程式を解く問題であった。)

