問題
問1
以下の極限値を求めよ。
\begin{eqnarray}
\lim_{n \to \infty}\left(\sqrt{n^2+4n}-n\right)
\end{eqnarray}
【解答はこちら】
問2
\(n\)が自然数で\(x\geq0\)の時、
(1)
以下の極限を求めよ。
\begin{eqnarray}
\lim_{n \to \infty}\frac{x^{n+3}-2x+3}{x^n}
\end{eqnarray}
(2)
(1)の極限値を\(f(x)\)とする時、\(y=f(x)\)のグラフを描け。
【解答はこちら】
問3
定数\(a\)は以下の範囲を満たす。
\begin{eqnarray}
0< a<4
\end{eqnarray}
この時、数列\({a_n}\)は以下の関係を満たす。
\begin{eqnarray}
a_1=2+\sqrt{a}\\
\\
a_n=2+\sqrt{a_{n-1}}
\end{eqnarray}
この時、以下の不等式を満たすことを示せ。
\begin{eqnarray}
0<4-a_n<\frac{4-a_{n-1}}{2}\tag{3.1}
\end{eqnarray}
また、以下の極限値も求めよ。
\begin{eqnarray}
\lim_{n \to \infty}a_n
\end{eqnarray}
【解答はこちら】
問4
以下の極限値を求めよ。
\begin{eqnarray}
\lim_{x \to 0}x\cos\frac{1}{x}
\end{eqnarray}
【解答はこちら】
問5
以下の極限値を求めよ。
\begin{eqnarray}
\lim_{x \to 0}\frac{\sin^22x}{1-\cos x}
\end{eqnarray}
【解答はこちら】
問6
以下の等式を満たす\(a,b\)を求めよ。
\begin{eqnarray}
\lim_{x \to \frac{\pi}{3}}\frac{a\sin x+b\cos x}{x-\frac{\pi}{3}}
\end{eqnarray}
【解答はこちら】
問7
\(a,b\)を定数とする。
この時、以下のような関数\(f(x)\)がある。
\begin{eqnarray}
f(x)=\lim_{n \to \infty}\frac{2x^{2x+1}+ax+b}{x^{2x+2}+4x^{2n}+5}
\end{eqnarray}
この時、関数\(f(x)\)が連続した関数である時、定数\(a,b\)の値を求めよ。
【解答はこちら】
解答
問1の解答 分子から平方根を外す
【問題はこちら】
分子分母に\(\sqrt{n^2+4n}+n\)をかける。
\begin{eqnarray}
\lim_{n \to \infty}&=&\frac{\left(\sqrt{n^2+4n}-n\right)\left(\sqrt{n^2+4n}+n\right)}{\sqrt{n^2+4n}+n}\\
\\
&=&\lim_{n \to \infty}\frac{4}{\sqrt{1+\frac{4}{n}}+1}
\\
&=&2
\end{eqnarray}
問2の解答 \(x\leq1\)と\(1\leq x\)の場合に分ける
【問題はこちら】
(1)
\(0\leq x<1\)の時、極限値は以下となる。
\begin{eqnarray}
\lim_{n \to \infty}\frac{x^{n+3}-2x+3}{x^n+1}&=&-2x+3
\end{eqnarray}
また、\(x>1\)の時、極限値は以下となる。
\begin{eqnarray}
\lim_{n \to \infty}\frac{x^3+\left(-2x+3\right)x^{-n}}{1+x^{-n}}=x^3
\end{eqnarray}
ここで、\(x=1\)の時、以下の等式を満たす。
\begin{eqnarray}
-2x+3=x^3
\end{eqnarray}
よって、極限値は以下となる。
\begin{eqnarray}
0\leq x\leq1の時&&-2x+3\\
\\
1\leq xの時&&x^3
\end{eqnarray}
(2)
関数\(f(x)\)をグラフにすると図2.1の様になる。
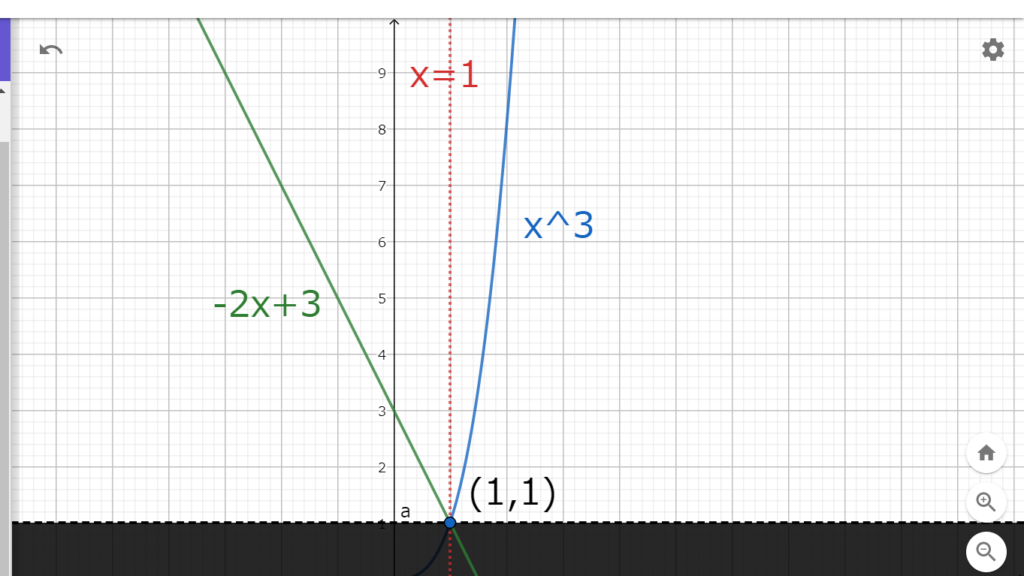 図2.1 関数f(x)のグラフ
図2.1 関数f(x)のグラフ関数\(f(x)\)は\(x=1\)で連続であり、\(0\leq x\leq1\)の範囲では\(y=-2x+3\)のグラフを描き、\(1\leq x\)の範囲では\(y=x^3\)のグラフを描く。
問3の解答 数学的帰納法を用いてからはさみうちの原理で極限値を求める
【問題はこちら】
まず、不等式3.1を示す。
不等式は数学的帰納法を用いて示す。
まず、\(n=2\)の時を考える。
以下の不等式が満たされるかを考える。
\begin{eqnarray}
0<4-a_2\\
\\
0<2-\sqrt{a_1}\\
\\
\sqrt{2+\sqrt{a}}<2
\end{eqnarray}
ここで、\(a<4\)より以上の不等式は満たされることが分かる。
次に以下の不等式が満たされるかを考える。
\begin{eqnarray}
4-a_n<\frac{4-a_{n-1}}{2}\\
\\
4-2\sqrt{a_1}<4-a_1\\
\\
\frac{a_1}{2}<\sqrt{a_1}
\end{eqnarray}
ここで、図3.1を考える。
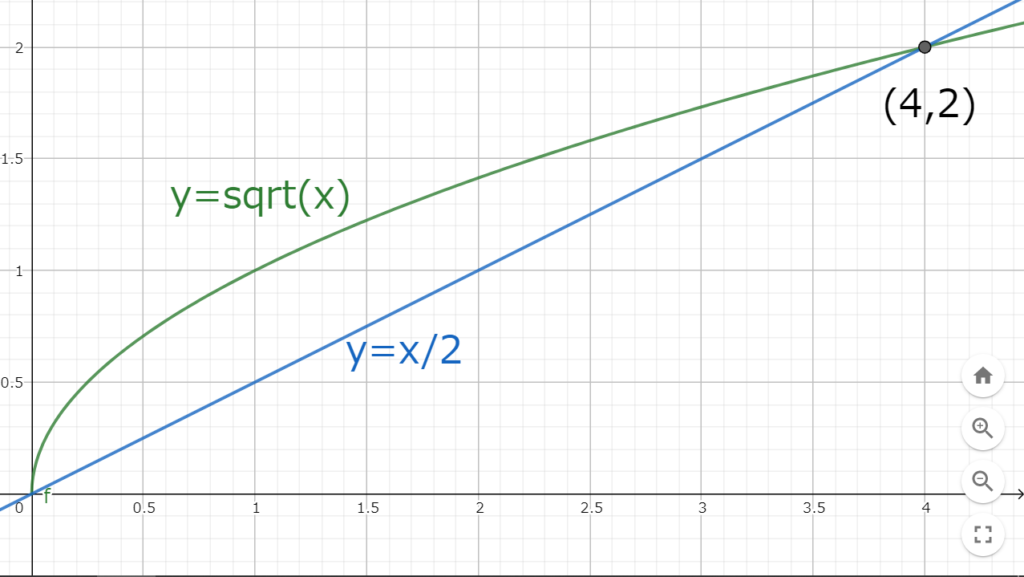 図3.1 y=x/2とy=√xのグラフ
図3.1 y=x/2とy=√xのグラフ\(y=\sqrt{x}\)は\(y=\frac{x}{2}\)よりも\(0< x<4\)の範囲で\(\sqrt{x}> \frac{x}{2}\)であることが分かる。
以上より、不等式3.1は\(n=2\)の時は満たされることが分かった。
次に\(n=k\)の時に不等式3.1が満たされると仮定する。
つまり、以下の不等式が満たされると仮定する。
\begin{eqnarray}
0<4-a_k<\frac{4-a_{k-1}}{2}\tag{3.2}
\end{eqnarray}
この時、\(n=k+1\)の時を考える。
まず、以下の不等式が成立するかを考える。
\begin{eqnarray}
0<4-a_{k+1}\\
\\
0<2-\sqrt{a_k}\\
\\
\sqrt{a_k}<2
\end{eqnarray}
ここで、不等式3.1より\(a_k<4\)を満たすことが分かる。
よって以上の不等式が成立することが分かる。
次に以下の不等式が成立するかを考える。
\begin{eqnarray}
4-a_{k+1}<\frac{4-a_k}{2}\\
\\
4-\left(2+\sqrt{a_k}\right)<\frac{4-a_k}{2}\\
\\
2\sqrt{a_k}>a_k\\
\\
4a_k>a_k^2
\end{eqnarray}
ここで、\(a_k>0\)なので不等式の両辺を二乗した。
ここで、不等式3.2から以下の不等式を満たすことが分かる。
\begin{eqnarray}
0<4-a_k\\
\\
a_k^2<4a_k
\end{eqnarray}
ここでも\(a_k>0\)なので\(a_k\)を両辺にかけた。
以上より、不等式を満たすことが分かった。
よって、\(n=k+1\)の時も不等式3.1を満たすことが分かった。
数学的帰納法より全ての\(n>2\)に対して不等式3.1は満たされることが分かった。
次に極限値を求める。
極限値の求め方は証明した不等式3.1を使ってはさみうちの原理から求める。
不等式3.1を式変形すると以下の様になる。
\begin{eqnarray}
0< a_n-4<\frac{4-a_{n-1}}{2}\\
\\
0> a_n-4>\frac{1}{2}\left(a_{n-1}-4\right)\tag{3.3}
\end{eqnarray}
ここで、以下の漸化式を考える。
\begin{eqnarray}
a_n-4=\frac{1}{2}\left(a_{n-1}-4\right)
\end{eqnarray}
ここで、新しい数列\(b_n=a_n-4\)と置くと数列\(b_n\)の一般項を以下の様になる。
\begin{eqnarray}
b_n=\left(\sqrt{a}-2\right)\left(\frac{1}{2}\right)^{n-1}
\end{eqnarray}
よって、数列\({a_n}\)の一般項は以下の様になる。
\begin{eqnarray}
a_n=\left(\sqrt{a}-2\right)\left(\frac{1}{2}\right)^{n-1}+4
\end{eqnarray}
なので、不等式3.3から以下の不等式を満たすことが分かる。
\begin{eqnarray}
4> a_n>\left(\sqrt{a}-2\right)\left(\frac{1}{2}\right)^{n-2}+4
\end{eqnarray}
ここで、以下の極限値を考える。
\begin{eqnarray}
\lim_{n \to \infty}\left(\left(\sqrt{a}-2\right)\left(\frac{1}{2}\right)^{n-2}+4\right)=4
\end{eqnarray}
よって、はさみうちの原理より数列\({a_n}\)の極限値は以下の様になる。
\begin{eqnarray}
\lim_{n \to \infty}a_n=4
\end{eqnarray}
問4の解答 \(\cos\)の範囲からはさみうちの原理
【問題はこちら】
\(\cos\frac{1}{x}\)は以下の範囲を満たす。
\begin{eqnarray}
0\leq\cos\leq1
\end{eqnarray}
ここで、両辺に\(x\)をかけると以下の様になる。
\begin{eqnarray}
0\leq x\cos\frac{1}{x}\leq x
\end{eqnarray}
ここで、\(x\)の極限値を計算する。
\begin{eqnarray}
\lim_{x \to 0}x=0
\end{eqnarray}
よって、はさみうちの原理より求める極限値は以下となる。
\begin{eqnarray}
\lim_{x \to 0}x\cos\frac{1}{x}=0
\end{eqnarray}
問5の解答 \(\lim_{x \to 0}\sin x\)の極限値を考える
【問題はこちら】
まず、分子分母に\(1+\cos x\)をかけると以下の様になる。
\begin{eqnarray}
\lim_{x \to 0}\frac{\sin^22x}{\left(1-\cos x\right)\left(1+\cos x\right)}&=&\left(\frac{\sin2x}{\sin x}\right)^2\left(1+\cos x\right)
\end{eqnarray}
ここで、\(\lim_{x \to 0}\sin x=x\)であるので、極限値は以下の様になる。
\begin{eqnarray}
\left(\frac{\sin2x}{\sin x}\right)^2\left(1+\cos x\right)&=&1^2\left(1+1\right)\\
\\
8
\end{eqnarray}
問6の解答 三角関数の合成から\(\theta\)を予想する
【問題はこちら】
まず、三角関数を\(r,\theta\)を用いて合成する。
\begin{eqnarray}
a\sin x+b\cos x=r\sin\left(x+\theta\right)\\
\\
但し、r=\sqrt{a^2+b^2},\cos\theta=\frac{a}{r},\sin\theta=\frac{b}{r}
\end{eqnarray}
よって、等式は以下のように変形できる。
\begin{eqnarray}
\lim_{x \to \frac{\pi}{3}}\frac{r\sin\left(x+\theta\right)}{x-\frac{\pi}{3}}=5\tag{6.1}
\end{eqnarray}
ここで、\(\theta=-\frac{\pi}{3}\)と仮定する。
すると式6.1は以下の様になる。
\begin{eqnarray}
\lim_{x \to \frac{\pi}{3}}\frac{r\sin\left(x-\frac{\pi}{3}\right)}{x-\frac{\pi}{3}}&=&\lim_{t \to 0}r\frac{\sin t}{t}\\
\\
&=&r=5
\end{eqnarray}
また、\(a,b\)は以下のことが成り立つ。
\begin{eqnarray}
\cos\left(-\frac{\pi}{3}\right)&=&\frac{1}{2}=\frac{a}{r}\\
\\
&&a=\frac{5}{2}
\end{eqnarray}
\begin{eqnarray}
\sin\left(-\frac{\pi}{3}\right)&=&-\frac{\sqrt{3}}{2}=\frac{b}{r}\\
\\
&&b=-\frac{5\sqrt{3}}{2}
\end{eqnarray}
この時の\(a,b\)は式6.1を満たすので以上の\(a,b\)が等式を満たす。
問7の解答 \(x=\pm1\)の時に同じ値を取るように\(a,b\)を決める
【問題はこちら】
\(x\)の範囲の場合分けによって関数\(f(x)\)を決める。
\(-1< x<1\)の時を考える。
関数\(f(x)\)は以下の様になる。
\begin{eqnarray}
f(x)=\lim_{n \to \infty}\frac{2x^{2x+1}+ax+b}{x^{2x+2}+4x^{2n}+5}=\frac{1}{5}\left(ax+b\right)
\end{eqnarray}
次に\(1< x\)の時を考える。
関数\(f(x)\)は以下の様になる。
\begin{eqnarray}
f(x)=\lim_{n \to \infty}\frac{2x+ax^{1-2x}+bx^{-2n}}{x^2+4+5x^{-2n}}=\frac{2x}{x^2+4}
\end{eqnarray}
次に\(x<-1\)の時を考える。
関数\(f(x)\)は以下の様になる。
\begin{eqnarray}
f(x)=\lim_{n \to \infty}\frac{2x+ax^{1-2x}+bx^{-2n}}{x^2+4+5x^{-2n}}=\frac{2x}{x^2+4}
\end{eqnarray}
ここで、\(x=1\)の時、関数\(f(x)\)は連続であることから以下の等式が成立する。
\begin{eqnarray}
\frac{1}{5}\left(a+b\right)=\frac{2}{5}\tag{①}
\end{eqnarray}
あmた、\(x=-1\)の時、関数\(f(x)\)は連続であることから以下の等式が成立する。
\begin{eqnarray}
\frac{1}{5}\left(b-a\right)=-\frac{2}{5}\tag{②}
\end{eqnarray}
ここ、①、②より\(a,b\)の連立方程式を解くと\(a,b\)は以下の様になる。
\begin{eqnarray}
a=2\\
b=0
\end{eqnarray}