本記事では、微分を用いて様々なことに応用していく。
まずは、平均値の定理について説明して、その証明も行っていく。
次に、微分を用いた関数の概形(関数の増減)について調べ方について説明する。
最後に、物理学などで用いる速度と加速度を位置の微分の形で表す方法について説明する。
微分を学んでも実際にどのように役立つかが本記事で掴むことができれば幸いである。
平均値の定理
平均値の定理は以下である。
平均値の定理
任意の関数\(f(x)\)が閉空間\([a,b]\)において連続であり、開空間\((a,b)\)において微分可能である時、
\begin{eqnarray}
\frac{f(b)-f(a)}{b-a}=f'(c)\\
\\
a<c<b
\end{eqnarray}
を満たす実数\(c\)が存在する。
証明
平均値の定理の証明をしていく。
まず、\(\frac{f(b)-f(a)}{b-a}\)の意味について考える。
図1.1のように横軸\(x\)、縦軸\(f'(x)\)の平面を考える。
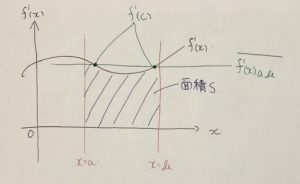 図1.1 f'(x)-x
図1.1 f'(x)-xここで、以下の定積分を見てみる。
\begin{eqnarray}
\int_{a}^{b}f'(x)dx=f(b)-f(a)
\end{eqnarray}
この定積分は図1.1の\(x=a,x=b,f'(x),y=0\)に囲まれた面積\(S\)である。
また、この定積分を\(b-a\)で割った値は面積\(S\)を横幅\(b-a\)にした時の高さに当たる。
言い換えると、\(x=a\)から\(x=b\)までの\(f'(x)\)の平均の値\(\overline{f'(x)_{a,b}}\)であることが分かる。
よって、以下のことが分かる。
\begin{eqnarray}
\overline{f'(x)_{a,b}}=\frac{1}{b-a}\int_{a}^{b}f'(x)dx
\end{eqnarray}
また、\(f(x)\)は連続であるので\(f'(x)\)も連続である。
よって、\(\overline{f'(x)_{a,b}}\)と等しい値を持つ\(a<c<b\)を満たす\(f'(c)\)が存在することが分かる。
つまり、以下の事が成立する。
\begin{eqnarray}
f'(c)&=&\overline{f'(x)_{a,b}}\\
\\
&=&\frac{1}{b-a}\int_{a}^{b}f'(x)dx\\
\\
&=&\frac{f(b)-f(a)}{b-a}
\end{eqnarray}
これで、平均値の定理の証明ができた。
微分を用いて関数の概形を調べる
本章では、微分を用いて関数の概形を調べていく。
本章で考えるのは一次導関数と二次導関数の正負である。
一次導関数は関数の接線の傾きである。
二次導関数は接線の傾きの増減具合である。
二次導関数の正負に分けて説明する。
\(f”(x)>0\)
\(f”(x)>0\)の時は、\(f'(x)\)が単調増加である。
よって、\(f'(x)\)は負から正へ増えていく。
関数\(f(x)\)の概形は図のように下に凸になる。
 図2.1 下に凸の関数f(x)
図2.1 下に凸の関数f(x)このような関数では\(f'(a)=0\)かつ\(f”(a)=0\)となる\(x\)が存在する。
この時、\(x<a\)では\(f'(x)<0\)、\(a<x\)では\(f'(x)>0\)となり、点\((a,f(a))\)のことを極小値と呼ぶ。
\(f”(x)<0\)
\(f”(x)<0\)の時は\(f'(x)\)が単調減少である。
よって、\(f'(x)\)は正から負へと減少していく。
関数\(f(x)\)の概形は図のように上に凸になる。
 図2.2 上に凸の関数f(x)
図2.2 上に凸の関数f(x)このような関数でも\(f'(a)=0\)かつ\(f”(a)=0\)となる\(x\)が存在する。
この時、\(x<a\)では\(f'(x)>0\)、\(a>x\)では\(f'(x)<0\)となり、点\((a,f(a))\)のことを極大値と呼ぶ。
\(f”(a)=0\)を満たす\((a,f(a))\)の前後で\(f”(x)\)の正負が変わる場合
この場合は、極小値も極大値も変わらず、\(f'(x)\)の正負も変わらない。
図のような\(f(x)=x^3\)などが例にある。
 図2.3 f(x)=x^3
図2.3 f(x)=x^3微分を用いた速度と加速度の表現
最後に、\(xy\)平面上を動く点の速度と加速度を微分を用いて表す。
\(xy\)平面上の点\(\overrightarrow{r}=\left(\begin{array}{c}x\\y\end{array}\right)\)が時刻\(t\)の関数である時、(つまり、\(x=x(t),y=y(t)\))点\(\overrightarrow{r}\)の速度\(\overrightarrow{v},\overrightarrow{\alpha}\)は以下のようになる。
\begin{eqnarray}
\overrightarrow{v}&=&\left(\begin{array}{c}\frac{dx}{dt}\\\frac{dy}{dt}\end{array}\right)\\
\\
\overrightarrow{\alpha}&=&\left(\begin{array}{c}\frac{d^2x}{dt^2}\\\frac{d^2y}{dt^2}\end{array}\right)
\end{eqnarray}
つまり、\(\overrightarrow{r(t)}=\left(\begin{array}{c}x(t)\\y(t)\end{array}\right)\)が分かれば、\(\overrightarrow{r(t)}\)を時刻\(t\)で微分することで速度\(\overrightarrow{v(t)}\)と加速度\(\overrightarrow{\alpha(t)}\)を求めることができる。
また、速度\(\overrightarrow{v(t)}\)の\(x\)成分と\(y\)成分について\(t\)で積分すると、位置\(\overrightarrow{r(t)}=\left(\begin{array}{c}x(t)\\y(t)\end{array}\right)\)を求めることができる。
つまり、位置\(\overrightarrow{r(t)}\)、速度\(\overrightarrow{v(t)}\)、加速度\(\overrightarrow{\alpha(t)}\)のいずれかが分かっていれば、微積分を用いることで他の物理量の時間変化を求めることができる。
まとめ
本記事では、微分を用いて定理の証明をして、関数の概形を調べて、速度や加速度の表現をしてきた。
その内容を以下にまとめる。
-
平均値の定理
任意の関数\(f(x)\)が閉空間\([a,b]\)において連続であり、開空間\((a,b)\)において微分可能である時、
\begin{eqnarray}
\frac{f(b)-f(a)}{b-a}=f'(c)\\
\\
a<c<b
\end{eqnarray}
を満たす実数\(c\)が存在する。 - 関数\(f(x)\)の一次導関数\(f'(x)\)と二次導関数\(f”(x)\)の正負によって関数の概形を調べることができる。
- 位置\(\overrightarrow{r(t)}\)、速度\(\overrightarrow{v(t)}\)、加速度\(\overrightarrow{\alpha(t)}\)はそれぞれ時刻\(t\)で微積分を求めることで、互いの物理量の時間変化を求めることができる。
特に、大学の物理学では速度や加速度を位置の導関数で表現をするのは当たり前になってくる。
高校で以上のような表現方法に慣れておくと良いと思うし、高校物理学でも考え方が変わってくるだろう。
演習問題
\(xy\)平面上を運動している物体が存在する。
この時の加速度\(\overrightarrow{\alpha}\)は以下である。
\begin{eqnarray}
\overrightarrow{\alpha}=\left(\begin{array}{c}
0\\
-g
\end{array}\right)\\
g:正の定数
\end{eqnarray}
但し、\(t=0\)の時、
\begin{eqnarray}
\overrightarrow{v}(t=0)&=&\left(\begin{array}{c}
\sqrt{3}\\
1
\end{array}\right)\tag{1.1}\\
\\
\overrightarrow{r}(t=0)&=&\left(\begin{array}{c}
0\\
0
\end{array}\right)
\end{eqnarray}
この物体の運動について、
(i)速度\(\overrightarrow{v}(t)\)、位置\(\overrightarrow{r}(t)=\left(\begin{array}{c}\overrightarrow{x}(t)\\\overrightarrow{y}(t)\end{array}\right)\)を求めよ。
(ii)位置\(\overrightarrow{y}(t)\)の最大値とその時の\(t\)を求めよ。
(iii)\(t≠0\)の時、\(y=0\)を満たす\(t\)を\(t=t_1\)とする。
ここで、\(t=0\)から\(t=t_1\)までの物体の\(y\)成分の平均の速度を\(v_y(t_c)\)とした時、\(t_c\)を求めよ。
加速度\(\overrightarrow{\alpha}(t)\)を時間\(t\)で積分すると速度\(\overrightarrow{v}(t)\)となり、更に速度\(\overrightarrow{v}(t)\)を時間\(t\)で積分すると位置\(\overrightarrow{r}(t)\)になる。
まずは、速度\(\overrightarrow{v}(t)\)を計算する。
\begin{eqnarray}
\overrightarrow{v}&=&\int\overrightarrow{\alpha}dt\\
\\
&=&\left(\begin{array}{c}
0\\
-gt
\end{array}\right)+\left(\begin{array}{c}
c_x\\
c_y
\end{array}\right)\\
\\
&&c_x,c_y:定数
\end{eqnarray}
ここで、式1.1を考えると(つまり、\(t=0\)の時を考える)以下のように定数\(c_x,c_y\)を求めることができる。
\begin{eqnarray}
\overrightarrow{v}(t=0)&=&\left(\begin{array}{c}
c_x\\
c_y
\end{array}\right)\\
\\
&=&\left(\begin{array}{c}
\sqrt{3}\\
1
\end{array}\right)
\end{eqnarray}
よって、速度\(\overrightarrow{v}(t)\)は以下になる。
\begin{eqnarray}
\overrightarrow{v}(t)&=&\left(\begin{array}{c}
\sqrt{3}\\
-gt+1
\end{array}\right)
\end{eqnarray}
次に、速度\(\overrightarrow{v}(t)\)を時間\(t\)で積分して位置\(\overrightarrow{r}(t)\)を求める。
速度\(\overrightarrow{v}(t)\)を積分すると以下になる。
\begin{eqnarray}
\overrightarrow{r}(t)&=&\int\overrightarrow{v}(t)dt\\
\\
&=&\left(\begin{array}{c}
\sqrt{3}t\\
-\frac{1}{2}gt^2+t
\end{array}\right)+\left(\begin{array}{c}
C_1\\
C_2
\end{array}\right)\\
\\
&&C_1,C_2:定数
\end{eqnarray}
ここで、式1.2を考えると(つまり、\(t=0\)の時の位置\(\overrightarrow{r}\)を考える)定数\(C_1,C_2\)は以下になる。
\begin{eqnarray}
\overrightarrow{r}(t)&=&\left(\begin{array}{c}
c_1\\
C_2
\end{array}\right)\\
&=&\left(\begin{array}{c}
0\\
0
\end{array}\right)
\end{eqnarray}
よって、位置\(\overrightarrow{r}(t)\)は以下のようになる。
\begin{eqnarray}
\overrightarrow{r}(t)&=&\left(\begin{array}{c}
\sqrt{3}t\\
-\frac{1}{2}gt^2+t
\end{array}\right)
\end{eqnarray}
(ii)
先で求めたように\(y(t)=-\frac{1}{2}gt^2+t\)である。
この\(y(t)\)を時間\(t\)についての一次導関数と二次導関数を求めて、それらの正負から関数の概形を求める。
だが、ここで\(y(t)\)の一次導関数と二次導関数はそれぞれ速度\(\overrightarrow{v}\)の\(y\)成分と加速度\(\overrightarrow{\alpha}\)の\(y\)成分である。
つまり、以下である。
\begin{eqnarray}
\frac{dy(t)}{dt}&=&-gt+1\\
\\
\frac{d^2y(t)}{dt^2}&=&-g
\end{eqnarray}
よって、\(y(t)\)の概形は図のようにかける。
 図5.1 y(t)-tのグラフと最大値
図5.1 y(t)-tのグラフと最大値よって、\(y(t)\)の最大値は\(t=\frac{1}{g}\)の時、\(\frac{1}{2g}\)である。
(iii)
まず、\(t_1\)を求める。
\(y(t)=0\)の場合を考える。
\begin{eqnarray}
&&-\frac{1}{2}gt^2+t=0\\
\\
&&t\left(-\frac{1}{2}gt+1\right)=0\\
\\
&&t=0,\frac{2}{g}\\
\\
&&t_1≠0より、\\
&&t_1=\frac{2}{g}
\end{eqnarray}
次に\(t=0\)から\(t=t_1\)までの平均の速度\(v_{ave}\)を求める。
\begin{eqnarray}
v_{ave}&=&\frac{t(t_1)-y(0)}{t_1-0}\\
\\
&=&-\frac{1}{2}gt_1+1\\
\\
&=&0
\end{eqnarray}
ここで、縦軸を\(v_y(t)\)、横軸を\(t\)とすると図のようなグラフになる。
 図5.2 v_y(t)-tのグラフ
図5.2 v_y(t)-tのグラフこの平均の速度\(v_{ave}\)はある速度\(v_y(t_c)\)と等しいので以下の等式を満たし、\(t_c\)を求めることができる。
\begin{eqnarray}
&&v_{ave}=v_y(t_c)\\
\\
&&-gt_c+1=0\\
\\
&&t_c=\frac{1}{g}
\end{eqnarray}
ここで、\(t_c\)は以下の2つの条件を満たした。
\begin{eqnarray}
&&\frac{y(t_1)-y(0)}{t_1-0}=\frac{dy(t_c)}{dt}\\
\\
&&0<t_c<t_1
\end{eqnarray}
よって、平均値の定理を満たしていることが分かる。