積分とはなんだろう。
一言でいうと、積分とは微小な値を足し合わせる計算である。
つまり、たし算と同じである。
図1のような、斜線部の面積を求めたいとする。
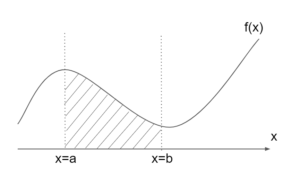 図1.関数f(x)、x=a、x=b、x軸に囲まれた斜線部の範囲
図1.関数f(x)、x=a、x=b、x軸に囲まれた斜線部の範囲関数\(f(x)\)のように曲線を描くような関数からできる面積を求めることは難しい。
だが、積分を用いると、このような面積を簡単に求めることができる。
本記事では、積分についてのイメージと計算方法について説明する。
積分のイメージ 微小の値を足し合わせる
積分とは、どのような考え方なのか見てみる。
図1のグラフを考える。
図1の斜線部は、\(x=a,x=b,f(x),x軸\)に囲まれた範囲である。
この斜線部の面積を積分を使って計算してみる。
ここで、\(x=a\)から\(x=b\)までを縦に分解した長方形の集まりと考えてみる。(図2)
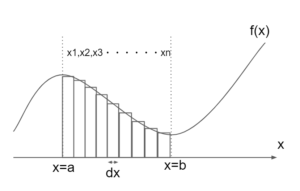 図2.斜線部の範囲を幅dxの長方形で分けた図
図2.斜線部の範囲を幅dxの長方形で分けた図このときの、長方形の幅は全て等しく\(dx\)になるように分解している。
そして、それぞれの長方形の\(x\)の値を\(x=a\)から\(x=b\)まで順に\(x_0,x_1,x_2,\cdots x_n\)とする。
次に、全ての長方形の面積の総和を考える。
長方形の面積の総和は数式で書くと、以下になる。
\begin{eqnarray}
長方形の面積の総和&=&f(x_0)dx+f(x_1)dx+\cdots +f(x_n)dx\\
\\
&=&\sum_{i=0}^n f(x_i)dx
\end{eqnarray}
長方形の面積の総和は、斜線部の面積と近い値を取るが、誤差があることがわかる。
なぜなら、斜線部の範囲は長方形で分解しているため、長方形の集まりでは完全に斜線部の範囲を表すことはできないからである。
ここで、\(dx\)の大きさに注目する。
\(dx\)とは長方形の幅である。
\(dx\)を小さくしていくと、長方形の集まりは斜線部の範囲をより正確に表すことができる。
つまり、長方形の面積の総和と斜線部の面積の誤差が小さくなることがわかる。
さらに、\(dx\)を\(0\)に近づけると、誤差は\(0\)に収束することもわかる。
よって、\(dx \xrightarrow[]{} 0\)の極限を取ると、長方形の面積の総和と、斜線部の面積は等しくなる。
\begin{eqnarray}
斜線部の面積=\lim_{dx \to 0}\sum_{i=0}^n f(x_i)dx
\end{eqnarray}
このように、微小な値\(dx\)を用いることで、近似的に求める計算方法を積分と呼ぶ。
ここでの左辺は、\(i=1\)から\(i=n\)までの長方形の面積を足し合わせている。
ここで、\(x_1=a,x_n=b\)である。
このとき、「\(x=a\)から\(x=b\)までを積分する」と言う。
それを、以下のように表現する。
\begin{eqnarray}
\lim_{dx \to 0}\sum_{i=0}^n f(x_i)dx=\int_{a}^{b}f(x)dx
\end{eqnarray}
積分の計算方法 微分の逆の計算
では、実際に積分の計算方法について説明する。
実は、積分は微分の計算の逆である。
まずは、微分についておさらいする。
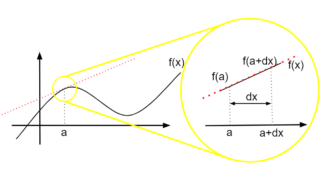
微分とは、関数\(f(x)\)において、微小間\(x,x+dx\)での変化率である。
ここでは、関数\(F(x)\)の微分を\(f(x)\)とし、以下のように表せる。
\begin{eqnarray}
f(x)=\frac{F(x+dx)-F(x)}{dx}
\end{eqnarray}
ここで、右辺の分母にある\(dx\)を左辺に移動する。
\begin{eqnarray}
f(x)dx=F(x+dx)-F(x) \tag{①}
\end{eqnarray}
まずは、式①の左辺に注目する。
ここで、二つの条件について確認する。
- \(x\)は任意である
- \(dx\)は微小な値である
\(x\)は任意であることから、前章のように決められた範囲を幅\(dx\)の長方形に分けて、それぞれ\(x_0,x_2,\cdots x_n\)とすることができる。
ここでは、範囲を前章と同じように\(x=a\)から\(x=b\)とする。
\(x_0,x_1,\cdots x_n\)に対応した式①の左辺\(f(x)dx\)の総和を考える。
\begin{eqnarray}
f(x_0)dx+f(x_1)+f(x_2)dx\cdots +f(x_n)dx=\sum_{i=0}^n f(x_i)dx
\end{eqnarray}
このとき、\(dx\)は微小である。
これは、前章で求めたように関数\(f(x)\)の積分である。
よって、以下のように書き換えられる。
\begin{eqnarray}
\sum_{i=0}^n f(x_i)dx=\int_{a}^{b}f(x)dx \tag{②}
\end{eqnarray}
次に、式①の右辺を考える。
右辺も\(x_0,x_1,x_2\cdots x_n\)の総和を考える。
\begin{eqnarray}
\sum_{i=0}^n F(x_i+dx)-F(x_i)
\end{eqnarray}
ここで、\(x_i\)について考える。
\(x_0,x_1,\cdots x_n\)は\(x=a\)から\(x=b\)までの長方形の\(x\)座標である。
さらに、長方形の幅は\(dx\)である。
よって、\(x_0,x_1,\cdots x_n\)は以下のような関係がある。
\begin{eqnarray}
x_1&=&x_0+dx\\
x_2&=&x_0+2dx\\
\\\cdots
x_n&=&x_0+ndx
\end{eqnarray}
すると、式①の右辺の総和は以下のように計算できる。
\begin{eqnarray}
\sum_{i=0}^n F(x_i+dx)-F(x_i)&=&F(x_0+dx)-F(x_0)+F(x_0+2dx)-F(x_0+dx)\\
&&+F(x_0+3dx)-F(x_0+2dx)+F(x_0+4dx)-F(x_0+3dx)\\
\\\cdots
&&+F(x_0+ndx)-F(x_0+(n-1)dx)\\
\\
&=&F(x_0+ndx)-F(x_0)
\end{eqnarray}
ここで、\(x_0=a,x_0+ndx=b\)である。
よって、式①の右辺の総和は以下である。
\begin{eqnarray}
\sum_{i=0}^n F(x_i+dx)-F(x_i)=F(b)-F(a)\tag{③}
\end{eqnarray}
よって、式①、②、③より、関数\(f(x)\)の積分は以下のようにかける。
\begin{eqnarray}
\int_{a}^{b}f(x)dx=F(b)-F(a)
\end{eqnarray}
関数\(F(x)\)は微分すると、\(f(x)\)になる。
つまり、微分すると関数\(f(x)\)になるような関数\(F(x)\)を求めることで、\(f(x)\)の積分を計算できる。
そして、そのような関数\(F(x)\)を求めることこそが、積分の計算である。
これまでの積分では、決められた範囲\(x=a\)から\(x=b\)での積分を行ってきた。
これらの範囲を積分範囲と呼ぶ。
だが、積分範囲の始まりを定数とし、終わりを変数として考えることもできる。
そのような考え方を不定積分と呼ぶ。
一方で、本章のように決められた範囲を積分して計算することを定積分と呼ぶ。
次章では、不定積分について説明する。
不定積分
不定積分とは、積分範囲を定数と変数を使って表し、積分をすることで新しい関数を作る計算である。
実際に不定積分をしてみる。
まずは、関数\(f(x),F(x)\)を考える。
\(F(x)\)を微分すると\(f(x)\)になるとする。
\begin{eqnarray}
f(x)=\frac{F(x+dx)-F(x)}{dx}
\end{eqnarray}
次に、関数\(f(x)\)の積分を考える。
ここで、積分範囲を考える。
積分の始まりは\(x=c\)となる任意定数\(c\)から始まるとする。
積分の終わりは\(x=x’\)となる任意変数\(x’\)で終わるとする。
すると、関数\(f(x)\)の積分は以下になる。
\begin{eqnarray}
\int_{c}^{x’}f(x)dx=F(x’)-F(c)
\end{eqnarray}
ここで、\(c\)は定数であるので、\(F(c)\)も定数である。
\(F(x)\)を新しい定数\(-C\)とおく。
さらに、変数\(x’\)は任意であるので、\(x’=x\)とおく。
すると、関数\(f(x)\)の積分は以下になる。
\begin{eqnarray}
\int_{c}^{x’}f(x)dx=F(x)+C
\end{eqnarray}
これを不定積分と呼ぶ。
不定積分を計算することで、何がわかるのか。
それは、関数\(f(x)\)を積分して得られる関数の\(x\)による振る舞いである。
定数\(C\)によるので一意には決まらないが、変数\(x\)による変化の具合を知ることができる。
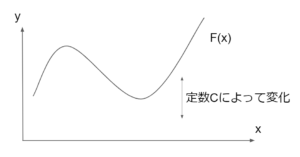 図3.不定積分で得た関数F(x)
図3.不定積分で得た関数F(x)不定積分は慣例的に以下のように書く。
\begin{eqnarray}
\int_{c}^{x’}f(x)dx=\int f(x)dx
\end{eqnarray}