問題
問1
以下の複素数関数\(f(z)\)がある。
\begin{eqnarray}
f(z)=z^4+az^3+bz^2+cz+d\\
(a,b,c,dは実数)
\end{eqnarray}
この時、\(f(z)=0\)となる方程式の解の一つが\(z=\alpha\)である時\(z=\overline{\alpha}\)も解であることを示せ。
【解答はこちら】
問2
\(z≠0\)の時、以下の値が実数であることを示せ。
\begin{eqnarray}
\frac{z}{|z|}+\frac{|z|}{z}\tag{2.1}
\end{eqnarray}
【解答はこちら】
問3
以下の複素数を極形式で表わせ。
\begin{eqnarray}
\sqrt{3}-\frac{1-i}{1+i}\tag{3.1}
\end{eqnarray}
【解答はこちら】
問4
以下の等式を満たす複素数zを求めよ。
\begin{eqnarray}
z^3=8i\tag{4.1}
\end{eqnarray}
【解答はこちら】
問5
複素平面上で点\(3+5i\)を点\(1+i\)の周りに正の向きで\(\frac{\pi}{3}\)だけ回転して得られる点を表す複素数を求めよ。
【解答はこちら】
問6
任意の複素数\(z\)に対して4点\(0,z,z^2,z^3\)を頂点とする四角形は正方形にならないことを証明せよ。
【解答はこちら】
問7
以下の複素数関数が描く図形を求めよ。
\begin{eqnarray}
3|z|=|z-\left(8-6i\right)|\tag{7.1}
\end{eqnarray}
【解答はこちら】
解答
問1の解答 関数\(f(z)\)の共役を考える
【問題はこちら】
複素数関数\(f(z)=0\)は\(z=\alpha\)を解に持つので以下の等式が成立する。
\begin{eqnarray}
f(\alpha)&=&\alpha^4+a\alpha^3+b\alpha^2+c\alpha+d\\
\\
&=&0
\end{eqnarray}
この時、\(\overline{f(\alpha)}\)を考える。
\begin{eqnarray}
\overline{f(\alpha)}&=&\underbrace{\overline{\alpha^4+a\alpha^3+b\alpha^2+c\alpha+d}}_{共役のバーを分解する}\\
\\
&=&\overline{0}=0
\end{eqnarray}
\begin{eqnarray}
\overline{\alpha^4+a\alpha^3+b\alpha^2+c\alpha+d}&=&\left(\overline{\alpha}\right)^4+a\left(\overline{\alpha}\right)^3+b\left(\overline{\alpha}\right)^2+c\left(\overline{\alpha}\right)+d\tag{1.1}\\
\\
&=&0
\end{eqnarray}
ここで、式1.1は\(f(\overline{\alpha})\)である。
よって\(f(\overline{\alpha})=0\)であるので\(\overline{\alpha}\)は方程式\(f(z)=0\)の解であることが分かる。
問2の解答 \(z+|z|\)の形を作る
【問題はこちら】
\(|z|^2=z\overline{z}\)から以下の関係が成立する。
\begin{eqnarray}
\frac{|z|}{z}=\frac{\overline{z}}{|z|}
\end{eqnarray}
よって、式2.1は以下の様になる。
\begin{eqnarray}
\frac{z}{|z|}+\frac{\overline{z}}{|z|}=\frac{1}{|z|}\left(z+\overline{z}\right)
\end{eqnarray}
ここで、\(|z|\)と\(z+\overline{z}\)は共に実数である。
よって、式2.1は実数である。
問3の解答 \(a+bi\)の形に直してから\(\theta,r\)を求める
【問題はこちら】
式3.1を\(a+bi\)の形に直すと以下の様になる。
\begin{eqnarray}
\sqrt{3}-\frac{\left(1-i\right)^2}{\left(1+i\right)\left(1-i\right)}&=&\sqrt{3}-\frac{1-2i+i^2}{1-i^2}\\
\\
&=&\sqrt{3}+i
\end{eqnarray}
ここで、実部を\(r\cos\theta\)、虚部を\(r\sin\theta\)と置く。
すると、それぞれ以下の値を取る。
\begin{eqnarray}
r\cos\theta&=&\sqrt{3}\\
\\
r\sin\theta&=&1
\end{eqnarray}
それぞれの2乗の和を取ると以下の様になる。
\begin{eqnarray}
r^2\cos^2\theta+r^2\sin^2\theta&=&r^2\\
\\
&=&\sqrt{3}^2+1^2\\
\\
&=&4
\end{eqnarray}
よって、\(r=2\)であることが分かる。
また、\(\cos\theta,\sin\theta\)は以下の値を取る。
\begin{eqnarray}
\cos\theta=\frac{\sqrt{3}}{2}\\
\\
\sin\theta=\frac{1}{2}
\end{eqnarray}
よって、\(\theta=\frac{\pi}{6}\)であることが分かる。
よって、求める式3.1は以下のように極形式で表すことができる。
\begin{eqnarray}
(式3.1)=2\cos\frac{\pi}{6}+2i\sin\frac{\pi}{6}
\end{eqnarray}
問4の解答 ド・モアブルの定理を使う
【問題はこちら】
複素数zを極形式で以下のように置く。
\begin{eqnarray}
z=r\left(\cos\theta+i\sin\theta\right)
\end{eqnarray}
すると、\(z^3\)はド・モアブルの定理を用いて以下のように式変形できる。
\begin{eqnarray}
z^3&=&r^3\left(\cos\theta+i\sin\theta\right)^3\\
\\
&=&r^3\left(\cos3\theta+i\sin3\theta\right)
\end{eqnarray}
ここで\(8i\)は極形式で表すと以下の様になる。
\begin{eqnarray}
8i=8\left(\cos\left(\frac{\pi}{2}+2n\pi\right)+i\sin\left(\frac{\pi}{2}+2n\pi\right)\right)\\
(nは整数)
\end{eqnarray}
よって、\(r=2,\theta=\frac{\pi}{6}+\frac{2}{3}n\pi\)となる。
よって、複素数zは以下の様になる。
\begin{eqnarray}
z=2\cos\left(\frac{\pi}{6}+\frac{2}{3}n\pi\right)+2i\sin\left(\frac{\pi}{6}+\frac{2}{3}n\pi\right)
\end{eqnarray}
ここで、\(0\leq\theta<2\pi\)とすると\(n=0,1,2\)の値を取る。
よって、複素数zは以下の3つの値を取る。
\begin{eqnarray}
z=\sqrt{3}+i,-\sqrt{3}+i,-2i
\end{eqnarray}
問5の解答 回転の中心を原点に合わせる
【問題はこちら】
点\(1+i\)を中心に点\(3+5i\)を回転させる前に\(1+i\)を原点に合わせる。
すると、図5.1の様に実部で\(-1\)、虚部で\(-1\)ずらす。
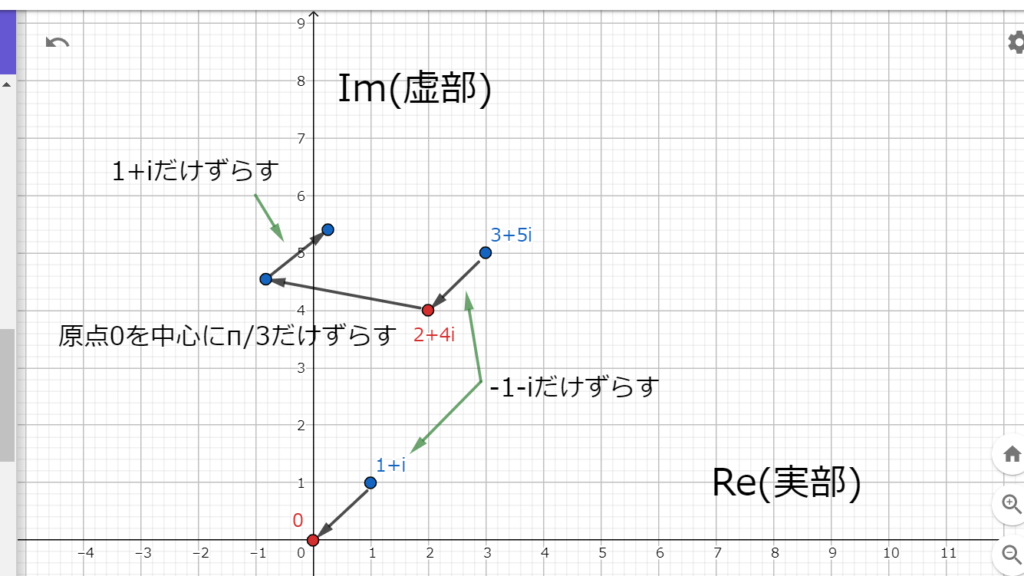 図5.1 点3+5iと点1+iを-1+iだけずらし、原点Oを中心にπ/3だけ2+4iを回転させた後、その点を1+iだけずらす
図5.1 点3+5iと点1+iを-1+iだけずらし、原点Oを中心にπ/3だけ2+4iを回転させた後、その点を1+iだけずらすすると、点\(3+5i\)は点\(2+4i\)に移る。
点\(2+4i\)を原点を中心にして\(\frac{\pi}{3}\)だけ回転させてから、実部を\(1\)、虚部を\(1\)だけずらして最初にずらした分をもとに戻す。
点\(2+4i\)を極形式で表すと\(2+4i=d\cos\theta+i\sin\theta\)となる。
この時、\(r,\theta\)はそれぞれ以下のように求められる。
\begin{eqnarray}
|2+4i|^2&=&r^2\\
\\
&=&2^2+4^2\\
\\
&=&20\\
↓\\
r&=&2\sqrt{5}
\end{eqnarray}
\begin{eqnarray}
\cos\theta&=&\frac{1}{\sqrt{5}}\\
\\
\sin\theta&=\frac{2}{\sqrt{5}}&
\end{eqnarray}
よって、\(2+4i=2\sqrt{5}\cos\theta+2\sqrt{5}i\sin\theta\)である。
次に点\(2+4i=2\sqrt{5}\cos\theta+2\sqrt{5}i\sin\theta\)を正の向きに\(\frac{\pi}{3}\)だけ回転させる。
これは、極形式において実軸との角度\(\theta\)に\(\frac{\pi}{3}\)だけ足した複素数となる。
よって、以下となる。
\begin{eqnarray}
2+4i=2\sqrt{5}\cos\theta+2\sqrt{5}i\sin\theta\xrightarrow[\frac{\pi回転}{3}]{}2+4i=2\sqrt{5}\cos\left(\theta+\frac{\pi}{3}\right)+2\sqrt{5}i\sin\left(\theta+\frac{\pi}{3}\right)
\end{eqnarray}
ここで、\(\cos\left(\theta+\frac{\pi}{3}\right),\sin\left(\theta+\frac{\pi}{3}\right)\)を加法定理を用いて計算する。
\begin{eqnarray}
\cos\left(\theta+\frac{\pi}{3}\right)&=&\cos\theta\cos\frac{\pi}{3}-\sin\theta\sin\frac{\pi}{3}\\
\\
&=&\frac{1}{\sqrt{5}}\cdot\frac{1}{2}-\frac{2}{\sqrt{5}}\cdot\frac{\sqrt{3}}{2}\\
\\
&=&\frac{1-2\sqrt{5}}{2\sqrt{5}}
\end{eqnarray}
\begin{eqnarray}
\sin\left(\theta+\frac{\pi}{3}\right)&=&\sin\theta\cos\frac{\pi}{3}+\sin\frac{\pi}{3}\cos\theta\\
\\
&=&\frac{2}{\sqrt{5}}\cdot\frac{1}{2}+\frac{\sqrt{3}}{2}\cdot\frac{1}{\sqrt{5}}\\
\\
&=&\frac{2+\sqrt{3}}{2\sqrt{5}}
\end{eqnarray}
よって、\(2+4i\)を正の向きに\(\frac{\pi}{3}\)だけ回転させた複素数の極形式は以下となる。
\begin{eqnarray}
r\cos\left(\theta+\frac{\pi}{3}\right)+i\sin\left(\theta+\frac{\pi}{3}\right)&=&\left(1-2\sqrt{3}\right)+\left(2+\sqrt{3}\right)i
\end{eqnarray}
最後に以上の点\(\left(1-2\sqrt{3}\right)+\left(2+\sqrt{3}\right)i\)を実部方向に\(+1\)、虚部方向に\(+1\)だけずらす。
すると、以下の様になる。
\begin{eqnarray}
\left(1-2\sqrt{3}\right)+\left(2+\sqrt{3}\right)i\xrightarrow[1+iを足す]{}\left(2-2\sqrt{3}\right)+\left(\sqrt{3}+3\right)i
\end{eqnarray}
よって、以上が求める複素数である。
問6の解答 極形式で表した\(r\)の場合分け
【問題はこちら】
複素数\(z\)を極形式で表すと\(z=r\left(\cos\theta+i\sin\theta\right)\)となる。
ここで、\(r\)が\(r=1,r≠1\)の時に場合分けして考える。
\(r=1\)
この時、以下の関係が成り立つ。
\begin{eqnarray}
|z|=|z^2|=|z^3|
\end{eqnarray}
ここで、点\(0\)を中心に考える。
すると、点\(z,z^3\)は点\(0\)と隣り合う点であり、点どうしを結ぶ線は四角形をなす辺である。
また、点\(z^2\)は点\(0\)と対角上にある点であり、点同士を結ぶ線は四角形の対角線をなす辺である。
だが、四角形の辺と対角線が等しい長さである正方形は存在しない。
四角形の辺と対角線の長さの比は必ず\(1:\sqrt{2}\)になる。
つまり、\(r=1\)の時、作り出される四角形は正方形にはならない。
\(r≠1\)
この時、以下の関係が成り立つ。
\begin{eqnarray}
|z|≠|z^3|
\end{eqnarray}
ここで点\(0\)を中心に考える。
すると、点\(z,z^3\)は点\(0\)と隣り合う点であり、点どうしを結ぶ線は四角形をなす辺である。
だが、四角形の辺の長さが違う。
よって、\(r≠1\)の時も作り出される四角形は正方形にはならない。
問7の解答 両辺を二乗して因数分解する
【問題はこちら】
式7.1の両辺を二乗すると以下の様になる。
\begin{eqnarray}
9z\overline{z}&=&\left(z-\left(8+6i\right)\right)\left(\overline{z}-\left(8-6i\right)\right)\\
\\
&=&z\overline{z}-z\left(8-6i\right)-\overline{z}\left(8+6i\right)+100\\
&&↓\\
8z\overline{z}+z\left(8-6i\right)+\overline{z}\left(8+6i\right)&=&100\\
&&↓\\
z\overline{z}+z\frac{4-3i}{4}+\overline{z}\frac{4+3i}{4}&=&\frac{25}{2}
\end{eqnarray}
ここで、左辺を因数分解すると以下の様になる。
\begin{eqnarray}
z\left(\overline{z}+\frac{4-3i}{4}\right)+\overline{z}\frac{4+3i}{4}+\underbrace{\frac{4+3i}{4}\frac{4-3i}{4}-\frac{25}{16}}_{足して0}&=&\frac{25}{2}\\
↓\\
\left(z+\frac{4+3i}{4}\right)\left(\overline{z}+\frac{4-3i}{4}\right)&=&\frac{175}{16}\\
↓\\
|z+\frac{4+3i}{4}|^2&=&\frac{175}{16}\\
↓\\
|z+\frac{4+3i}{4}|=\frac{5\sqrt{7}}{4}
\end{eqnarray}
よって、点\(-\frac{4+3i}{4}\)を中心とした半径\(\frac{5\sqrt{7}}{4}\)の円であることが分かる。

