問題
問1
以下の三次方程式をグラフを用いて解け。
\begin{eqnarray}
x^3-x\leq0
\end{eqnarray}
【解答はこちら】
問2
以下の方程式が3つの実数解を持つ時、定数aの値を求めよ。
\begin{eqnarray}
2x^3-9x+a=0
\end{eqnarray}
【解答はこちら】
問3
1>xの時以下の不等式が成り立つことを証明せよ。
\begin{eqnarray}
x^3-6x^2+13x-8>0
\end{eqnarray}
【解答はこちら】
問4
全ての正の数xに対して以下の不等式を満たすような定数aの最小値を求めよ。
\begin{eqnarray}
ax^3-3x^2+1\geq0
\end{eqnarray}
【解答はこちら】
解答
問1の解答 増減表からグラフを描く
【問題はこちら】
以下の様にf(x)を置く。
$$f(x)=x^3-x$$
ここで導関数f'(x)を求める。
\begin{eqnarray}
f^{\prime}(x)=3x^2+1
\end{eqnarray}
ここで導関数が0の時を調べる。
\begin{eqnarray}
f^{\prime}(x)&=&3x^2-1\\
&=&0\\
\\
x=\pm\frac{1}{\sqrt{3}}
\end{eqnarray}
よって、関数f(x)の増減表は以下となる。
| $$x$$ | $$\cdots$$ | $$-1$$ | $$\cdots$$ | $$-\frac{1}{\sqrt{3}}$$ | $$\cdots$$ | $$0$$ | $$\cdots$$ | $$\frac{1}{\sqrt{3}}$$ | $$\cdots$$ | $$1$$ | $$\cdots$$ |
| $$f^{\prime}(x)$$ | $$+$$ | $$+$$ | $$+$$ | $$0$$ | $$-$$ | $$-$$ | $$-$$ | $$0$$ | $$+$$ | $$+$$ | $$+$$ |
| $$f(x)$$ | $$↗$$ | $$0$$ | $$↗$$ | $$\frac{2\sqrt{3}}{9}$$ | $$↘$$ | $$0$$ | $$↘$$ | $$-\frac{2\sqrt{3}}{9}$$ | $$↗$$ | $$0$$ | $$↗$$ |
よって、関数f(x)は図1.1の様になる。
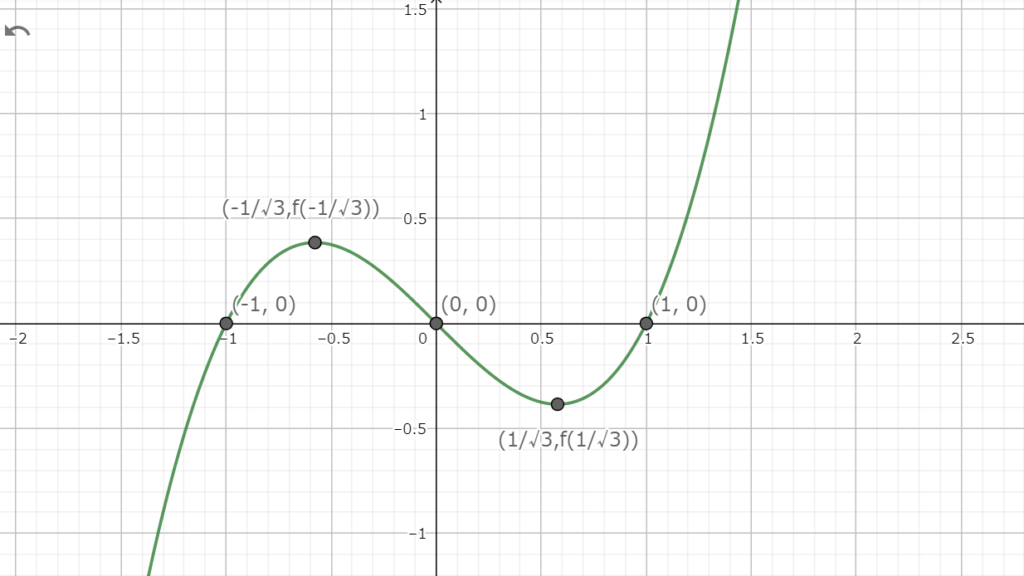 図1.1 関数f(x)の極値とf(x)=0の解
図1.1 関数f(x)の極値とf(x)=0の解よって、不等式を満たす範囲はこの関数f(x)が負になる範囲である。
よって、xの範囲は以下である。
\begin{eqnarray}
x\leq -1,0\leq x\leq1
\end{eqnarray}
問2の解答 極大値と極小値の範囲を考える
【問題はこちら】
まず、f(x)を以下の様に置く。
$$f(x)=2x^3-9x^2+a$$
ここで、導関数f'(x)を求める。
$$f^{\prime}(x)=6x^2-18x$$
導関数f'(x)が0の時を考える。
\begin{eqnarray}
f^{\prime}(x)&=&6x\left(x-3\right)\\
&=&0\\
\\
x=0,3
\end{eqnarray}
よって、関数f(x)の増減表は以下となる。
| $$x$$ | $$\cdots$$ | $$0$$ | $$\cdots$$ | $$3$$ | $$\cdots$$ |
| $$f^{\prime}(x)$$ | $$+$$ | $$0$$ | $$-$$ | $$0$$ | $$+$$ |
| $$f(x)$$ | $$↗$$ | $$a$$ | $$↘$$ | $$a-27$$ | $$↗$$ |
よって、関数f(x)は図2.1の様になる。
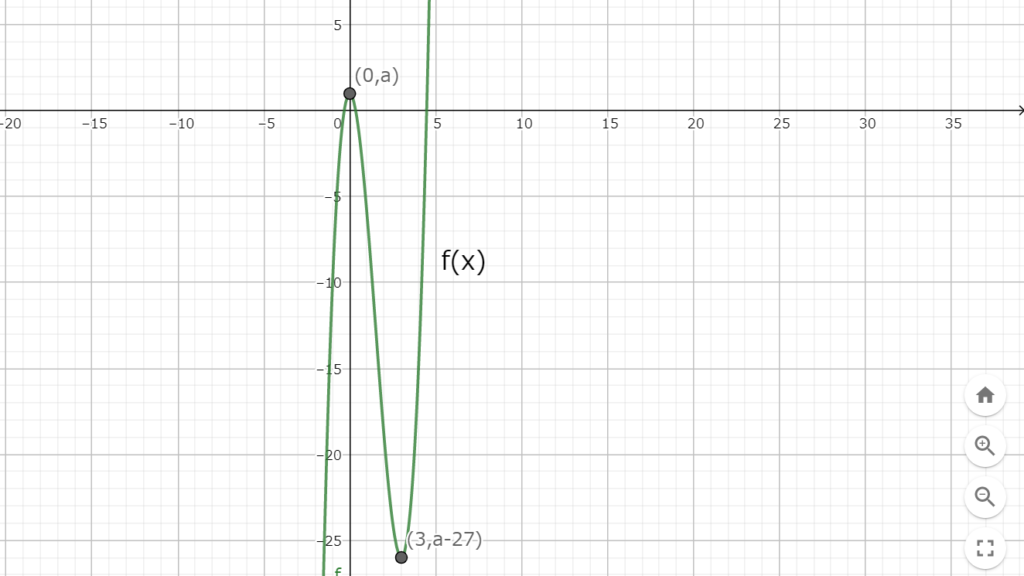 図2.1 関数f(x)の極値
図2.1 関数f(x)の極値この時、式2.1の方程式が3つの実数解を持つ時、極大値が正であり極小値が負である必要がある。
よって、定数aは以下の条件を満たす必要がある。
\begin{eqnarray}
0< a\\
\\
a-27<0\\
↓\\
0< a<27
\end{eqnarray}
式2.1の方程式が3つの実数解を持つためには定数aは以上の範囲を満たす必要がある。
問3の解答 f'(x)からf(x)が増加関数であることを示す
【問題はこちら】
関数f(x)を以下のように置く。
$$f(x)=x^3-6x^2+13x-8$$
導関数f'(x)を求める。
\begin{eqnarray}
f^{\prime}(x)&=&3x^2-12+13\\
&=&3\left(x-2\right)^2+1\tag{式3.1}
\end{eqnarray}
式3.1からf'(x)はxの値の依らず正の値を取ることが分かる。
つまり、関数f(x)は増加関数であることが分かる。
次にx=1の時の関数f(x=1)を考える。
\begin{eqnarray}
f(x=1)=0
\end{eqnarray}
ここで、関数f(x)は増加関数であるのでxが1以上の時関数f(x)は0以上であることが分かる。
よって、不等式を証明することができた。
問4の解答 最小値が正になるときを考える
【問題はこちら】
関数f(x)を以下のように置く。
\begin{eqnarray}
f(x)=ax^3-3x^2+1
\end{eqnarray}
導関数f'(x)を求める。
\begin{eqnarray}
f^{\prime}(x)=3ax^2-6x
\end{eqnarray}
ここで、f'(x)が0の時を考える。
\begin{eqnarray}
f^{\prime}(x)&=&3x\left(ax-2\right)\\
&=&0\\
\\
x=0,\frac{2}{a}
\end{eqnarray}
よって、関数f(x)の増減表は以下となる。
| $$x$$ | $$0$$ | $$\cdots$$ | $$\frac{2}{a}$$ | $$\cdots$$ |
| $$f^{\prime}(x)$$ | $$0$$ | $$-$$ | $$0$$ | $$+$$ |
| $$f(x)$$ | $$1$$ | $$↘$$ | $$1-\frac{4}{a^2}$$ | $$↗$$ |
よって、増減表から関数f(x)は図4.1の様になる。
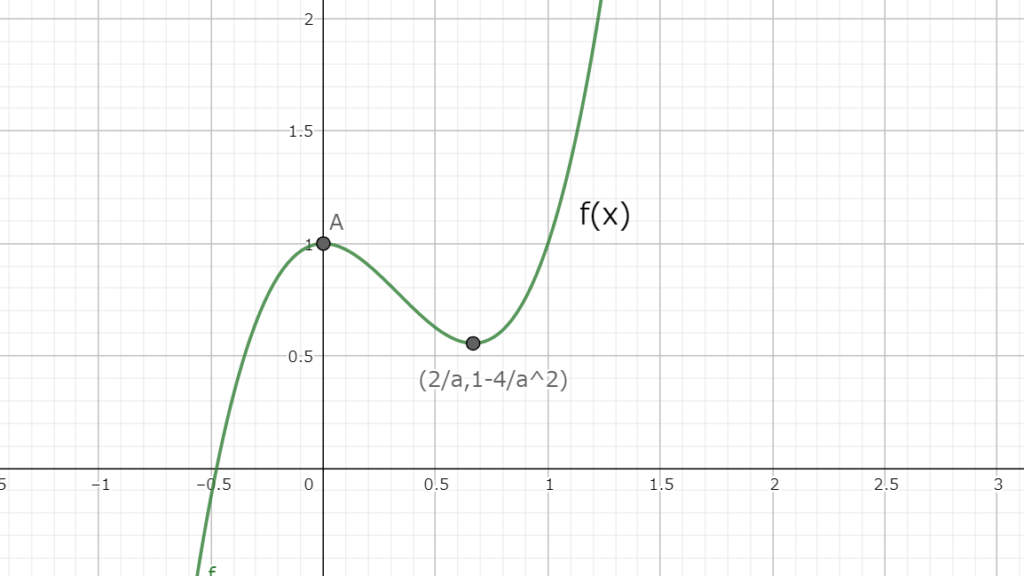 図4.1 関数f(x)の極値
図4.1 関数f(x)の極値この時、関数f(x)が全てのxに対して不等式を満たす時は最小値が0以上であることが必要である。
関数f(x)の最小値は極小値であり、以下である。
\begin{eqnarray}
最小値:1-\frac{4}{a^2}
\end{eqnarray}
この最小値が0以上でなければならない。
\begin{eqnarray}
1-\frac{4}{a^2}\geq0\\
\\
\left(1+\frac{2}{a}\right)\left(1-\frac{2}{a}\right)\geq0
\end{eqnarray}
ここで、a>0なので1+2/aは常に正である事が分かる。
よって、1-2/aが0以上である必要がある。
\begin{eqnarray}
1-\frac{2}{a}\geq0\\
↓\\
a\geq2
\end{eqnarray}
よって、全てのxに対して不等式を満たすような定数aの最小値は2である。

