問題
問1
次の値を求めよ。
$$\sinθ+\sin\left(θ+\frac{2}{3}\pi\right)+\sin\left(θ+\frac{4}{3}\pi\right)\tag{式1.1}$$
【解答はこちら】
問2
以下の方程式の直線となす角が\(\frac{\pi}{3}\)であり原点を通る直線の方程式を求めよ。
$$y=x+1\tag{式2.1}$$
【解答はこちら】
問3
次の等式を証明せよ。
$$\left(\sinθ-\cosθ\right)^2=1-\sin2θ\tag{式3.1}$$
【解答はこちら】
問4
次の式をrsin(θ+α)の形で表わせ。
\begin{eqnarray}
\sinθ-\sqrt{3}\cosθ\tag{式4.1}\\
\left(-\pi< θ <\pi\right)
\end{eqnarray}
【解答はこちら】
問5
次の不等式を解け。
\begin{eqnarray}
\cos2θ>\sinθ\tag{式5.1}\\
\left(0\leq θ<2\pi\right)
\end{eqnarray}
【解答はこちら】
問6
以下の関数の最大値と最小値、またその時のθを求めよ。
\begin{eqnarray}
y=4\sinθ-\cos2θ+3\tag{式6.1}\\
\left(0\leq θ<2\pi\right)
\end{eqnarray}
【解答はこちら】
問7
次の関数の最大値と最小値とその時のxを求めよ。
\begin{eqnarray}
y=-\sin x+\cos x\\
\left(0\leq x<2\pi\right)
\end{eqnarray}
【解答はこちら】
解答
問1の解答 加法定理の計算
【問題はこちら】
加法定理を使って2項目と3項目を計算していく。
まず、2項目の計算は以下となる。
\begin{eqnarray}
\sin\left(θ+\frac{2}{3}\pi\right)&=&\sinθ\cos\frac{2}{3}\pi+\sin\frac{2}{3}\pi\cosθ\\
&=&-\frac{1}{2}\sinθ+\frac{\sqrt{3}}{2}\cosθ\tag{①}
\end{eqnarray}
次に3項目の計算は以下となる。
\begin{eqnarray}
\sin\left(θ+\frac{4}{3}\pi\right)&=&\sinθ\cos\frac{4}{3}\pi+\sin\frac{4}{3}\pi\cosθ\\
&=&-\frac{1}{2}\sinθ-\frac{\sqrt{3}}{2}\cosθ\tag{②}
\end{eqnarray}
よって、①、②から式1.1は以下のように計算できる。
\begin{eqnarray}
(式1.1)&=&\sinθ+①+②\\
&=&0
\end{eqnarray}
問2の解答 直線の傾きは直線とx軸がなす角度\(\alpha\)の\(\tan\alpha\)と等しい
【問題はこちら】
式2.1の直線の傾きは1なので式2.1は以下のように書き換えられる。
$$(式2.1)=\tan\frac{\pi}{4}$$
ここで、式2.1となす角度が\(\frac{\pi}{3}\)であり原点を通る直線の傾きは以下の様に表すことができる。
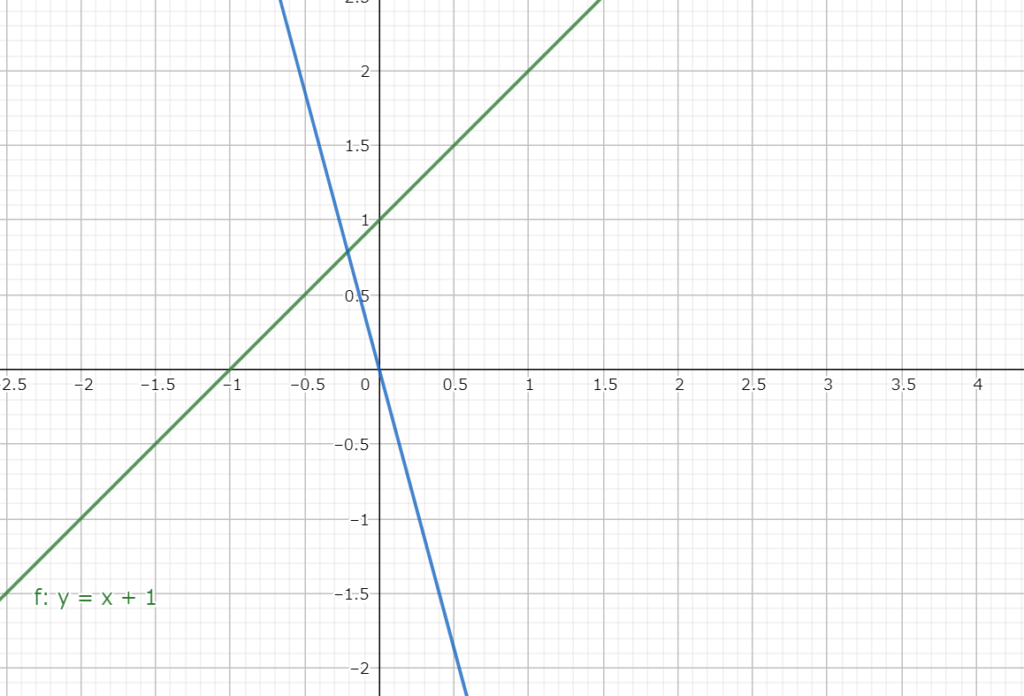 図2.1 y=x+1(緑線)とのなす角がπ/3で原点を通る直線(青線)
図2.1 y=x+1(緑線)とのなす角がπ/3で原点を通る直線(青線)$$(直線の傾き)=\tan\left(\frac{\pi}{4}\pm\frac{\pi}{3}\right)\tag{③}$$
よって、③の値をtanの加法定理を使って求める。
+の場合
\begin{eqnarray}
\tan\left(\frac{\pi}{4}+\frac{\pi}{3}\right)&=&\frac{\tan\frac{\pi}{4}+\tan\frac{\pi}{3}}{1+\tan\frac{\pi}{4}\tan\frac{\pi}{3}}
&=&\frac{1+\sqrt{3}}{1-\sqrt{3}}\\
&=&-\frac{1}{2}\left(1+2\sqrt{3}+3\right)\\
&=&-2-\sqrt{3}\tag{④}
\end{eqnarray}
-の場合
\begin{eqnarray}
\tan\left(\frac{\pi}{4}+\frac{\pi}{3}\right)&=&\frac{\tan\frac{\pi}{4}-\tan\frac{\pi}{3}}{1-\tan\frac{\pi}{4}\tan\frac{\pi}{3}}\\
&=&\frac{1-\sqrt{3}}{1-\sqrt{3}}\\
&=&-\frac{1}{2}\left(1-2\sqrt{3}+3\right)\\
&=&-2+\sqrt{3}\tag{⑤}
\end{eqnarray}
④、⑤より求める直線の方程式は以下となる。
\begin{eqnarray}
y=-\left(2+\sqrt{3}\right)x\\
\\
y=\left(-2+\sqrt{3}\right)x
\end{eqnarray}
問3の解答 倍角の公式を用いる
【問題はこちら】
式3.1の左辺を展開すると以下の様になる。
\begin{eqnarray}
\left(\sinα-\cosα\right)^2&=&\sin^2α-2\sinα\cosα+\cos^2α\\
&=&1-2\sinα\cosα\tag{⑥}
\end{eqnarray}
ここで、sinの倍角の公式を見てみる。
\begin{eqnarray}
\sin2α&=&\sinα\cosα+\sinα\cosα\\
&=&2\sinα\cosα\tag{⑦}
\end{eqnarray}
ここで、⑥に⑦を代入すると以下になる。
\begin{eqnarray}
⑥=1-2\sinα\cosα
\end{eqnarray}
よって、式3.1を証明できた。
問4の解答 三角関数の合成
【問題はこちら】
式4.1のsinθとcosθの係数をそれぞれaとbとする。
この時、aとbからrを求める。
\begin{eqnarray}
r&=&\sqrt{a^2+b^2}\\
&=&\sqrt{1^2+\left(-\sqrt{3}\right)}\\
&=&2
\end{eqnarray}
ここで、a,b,rから\(cos\alpha,sin\alpha\)を求める。
\begin{eqnarray}
\cosα&=&\frac{a}{r}\\
&=&\frac{1}{2}\\
\\
\sinα&=&\frac{b}{r}\\
&=&-\frac{\sqrt{3}}{2}
\end{eqnarray}
よって、\(\alpha\)は以下の値となる。
$$α=-\frac{\pi}{3}$$
よって、式4.1は以下のように書き換えられる。
$$(式4.1)=2\sin\left(θ-\frac{\pi}{3}\right)$$
問5の解答 sinθの二次不等式に書き換える
【問題はこちら】
まず、cos2θをsinθに書き換える。
\begin{eqnarray}
\cos2θ&=&\cos^2θ-\sin^2θ\\
&=&\left(1-\sin^2θ\right)-\sin^2θ\\
&=&1-2\sin^2θ\tag{⑧}
\end{eqnarray}
⑧を式5.1に代入して整理すると以下のようなsinθの二次不等式になる。
\begin{eqnarray}
1-2\sin^2θ>\sinθ\\
\\
2\sin^2θ+\sinθ-1<0\tag{式5.2}
\end{eqnarray}
ここで、式5.2が0となる時の二次方程式を考える。
\begin{eqnarray}
(式5.2)=\left(2\sinθ-1\right)\left(\sinθ+1\right)=0\\
\\
\sinθ=\frac{1}{2},-1
\end{eqnarray}
グラフにすると図5.1のようなグラフとなる。
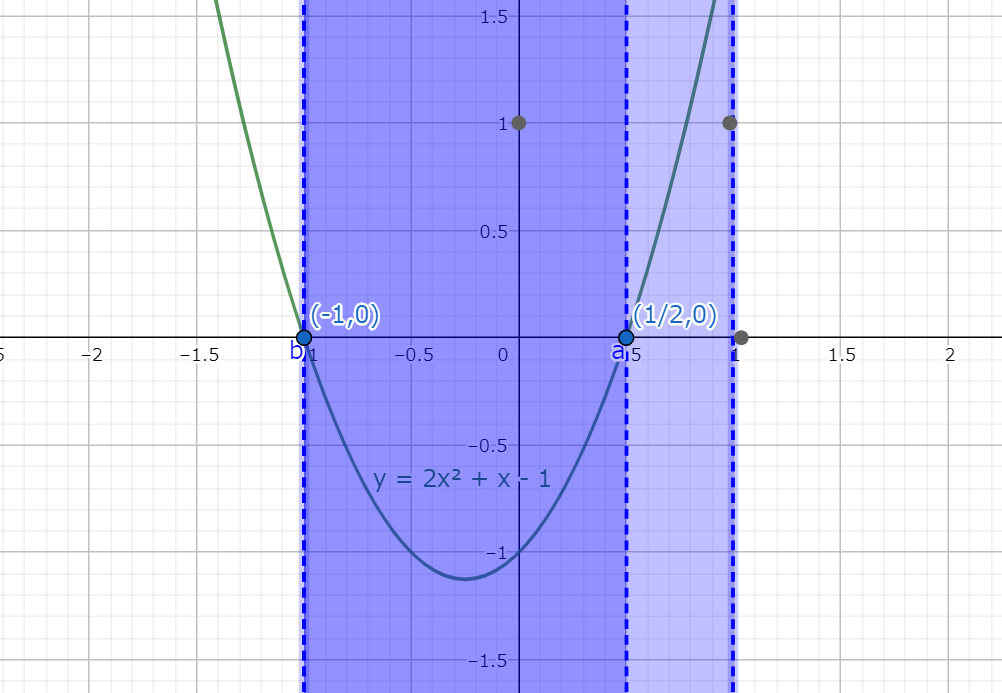 図5.1 式5.2の不等式の結果(濃い範囲が二次不等式の結果)
図5.1 式5.2の不等式の結果(濃い範囲が二次不等式の結果)更に、θの範囲からsinθは-1以上1以下となる。
よって、式5.1の不等式の解(図5.1で言うとグラフが負になっている範囲)は以下となる。
\begin{eqnarray}
-1<\sinθ<\frac{1}{2}\\
\\
0\leq θ<\frac{\pi}{6},\frac{5}{6}\pi< θ<2\pi
\end{eqnarray}
関連単元
【二次不等式とは】
問6の解答 sinθの二次方程式からグラフ化する
【問題はこちら】
最初に式6.1を問5のようにsinθの二次方程式にする。
cos2θを書き換えると⑧のようになるので式6.1は以下のように書き換えられる。
\begin{eqnarray}
(式6.1)&=&4\sinθ-\left(1-2\sin^2θ\right)+3\\
&=&2\sin^2θ+4\sinθ+2\\
&=&2\left(\sinθ+1\right)^2
\end{eqnarray}
ここで、式6.1が0の値を取る時の二次方程式を考える。
二次方程式の解は以下となる。
\begin{eqnarray}
\sinθ=-1\\
\left(θ=\frac{3}{2}\pi\right)
\end{eqnarray}
グラフで描くと図6.1の様になる。
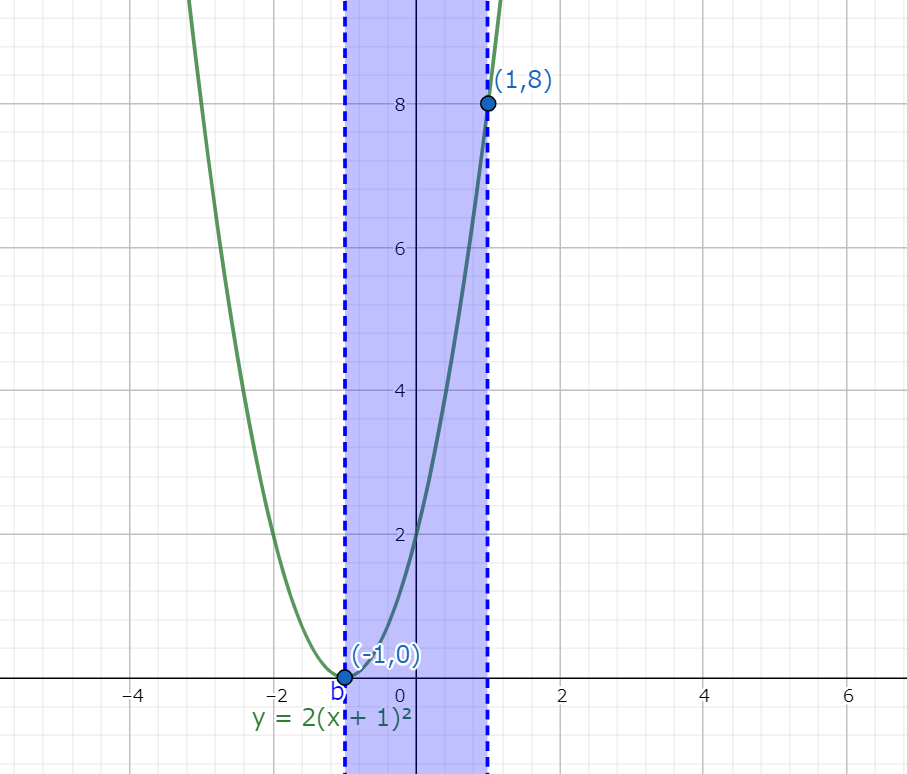 図6.1 式6.1のグラフとsinθの範囲(青い範囲)
図6.1 式6.1のグラフとsinθの範囲(青い範囲)更にθの範囲からsinθの範囲は-1以上1以下となる。
よって、式6.1の最大値、最小値は以下となる。
\begin{eqnarray}
最大値&:&8\left(θ=\frac{\pi}{2}\right)
最小値&:&0\left(θ=\frac{3}{2}\pi\right)
\end{eqnarray}
問7の解答 xの範囲を拡張する
【問題はこちら】
最初に式7.1を問4のように三角関数の合成を行う。
まず、rを求める。
\begin{eqnarray}
r&=&\sqrt{\left(-1\right)^2+1^2}\\
&=&\sqrt{2}
\end{eqnarray}
次にsinx、cosxの係数a,bと求めたrから\(cos\alpha,sin\alpha\)を求める。
\begin{eqnarray}
\cosα=-\frac{1}{\sqrt{2}}\\
\sinα=\frac{1}{2}
\end{eqnarray}
よって、\(\alpha=\frac{3}{4}\pi\)であることが分かる。
式7.1を合成すると以下の様になる。
$$(式7.1)=\sqrt{2}\sin\left(x+\frac{3}{4}\pi\right)\tag{式7.2}$$
ここで、最大値と最小値を考える。
sinは周期関数であるので式7.2の最大値と最小値は\(\sin(x+\frac{3}{4}\pi)\)がそれぞれ1と-1を取る時である事が分かる。
次に式7.2が最大値と最小値を取るxについて考える。
まず、最大値について考える。
式7.2が最大値を取る時の条件は以下である。
\begin{eqnarray}
\sin\left(x+\frac{3}{4}π\right)=1\\
\\
x+\frac{3}{4}\pi=\frac{\pi}{2}\\
x=-\frac{\pi}{4}
\end{eqnarray}
だが、この時のxはxの範囲を満たしていない。
よって、ここでxの解を以下の様に拡張する。
\begin{eqnarray}
x+\frac{3}{4}\pi=\frac{\pi}{2}+2n\pi\\
(n=0,1,2,3,・・・)\\
x=-\frac{\pi}{4}+2n\pi\tag{⑨}
\end{eqnarray}
⑨のようにxの解を拡張したするとn=1の時にxの範囲を満たす解を得られる。
よって、式7.1の最大値はxが以下の時である。
$$x=\frac{7}{4}\pi$$
同様に最小値についても考える。
式7.2が最小値を取る時の条件は以下である。
\begin{eqnarray}
\sin\left(x+\frac{3}{4}π\right)=-1\\
\\
x+\frac{3}{4}\pi=\frac{3}{2}\pi+2n\pi\\
(n=0,1,2,3,・・・)\\
x=\frac{3}{4}\pi+2n\pi\\
\\
n=0の時
x=\frac{3}{4}\pi
\end{eqnarray}
よって式7.1の最小値はxが以下の時である。
$$x=\frac{3}{4}\pi$$
まとめると式7.1の最大値と最小値は以下の様になる。
\begin{eqnarray}
最大値&:&\sqrt{2} \left(x=\frac{7}{4}\pi\right)\\
最小値&:&-\sqrt{2} \left(x=\frac{3}{4}\pi\right)
\end{eqnarray}
グラフにすると図7.1の様になる。
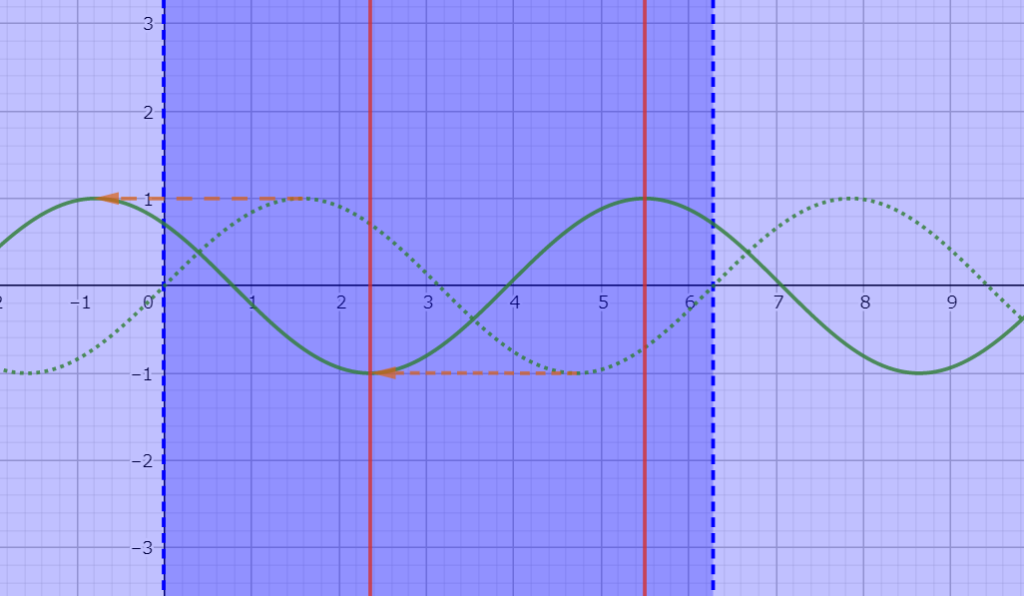 図7.1 sinxをsin(x+3π/4)ずらしたグラフとその時に最大値と最小値を取るxの値
図7.1 sinxをsin(x+3π/4)ずらしたグラフとその時に最大値と最小値を取るxの値
