不定積分
公式
積分の定義
\(F'(x)=f(x)\)の時
\begin{eqnarray}
\int f(x)dx=F(X)+C\\
(Cは定数)
\end{eqnarray}
べき乗関数の積分
\begin{eqnarray}
\int x^ndx=\frac{x^{n+1}}{n+1}+C
\end{eqnarray}
不定積分の性質
\(F'(x)=f(x),G(x)=g(x)\)の時
\begin{eqnarray}
\int kf(x)dx&=&k\int f(x)dx\\
\\
\int {f(x)\pm g(x)}dx&=&F(x)\pm G(x)+C
\end{eqnarray}
定積分
公式
定積分の定義
\(F'(x)=f(x)\)の時
\begin{eqnarray}
\int_{a}^{b}f(x)dx=F(b)-F(a)
\end{eqnarray}
定積分を図で表すと図1.1の様になる。
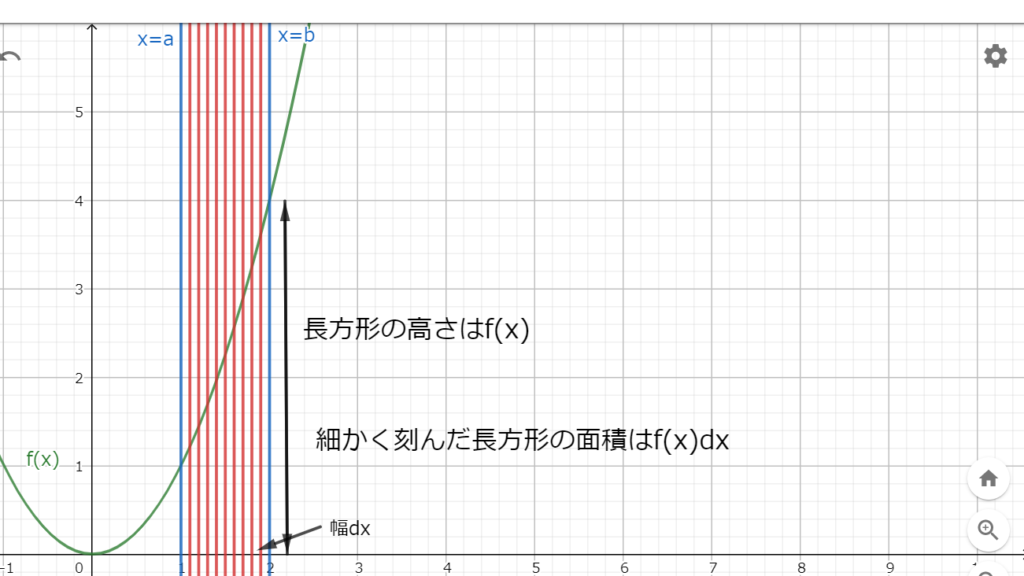 図1.1 関数f(x)をx=aからx=bまで微小な幅dxで刻んだ図
図1.1 関数f(x)をx=aからx=bまで微小な幅dxで刻んだ図まず、関数\(f(x)\)を積分範囲である\(x=a\)から\(x=b\)まで範囲を考える。
\(x=a\)から\(x=b\)までを\(x\)について限りなく0に近い幅である\(dx\)で均等に分割する。
すると、\(x\)軸と関数\(f(x)\)の間に無数の長方形が\(x=a\)から\(x=b\)の間にできる。
この長方形の一つ一つの面積は\(f(x)dx\)である。
この無数の長方形の面積を足し合わせる事が積分という作業であり、積分を計算した結果は\(x\)軸と関数\(f(x)\)の間の面積になる。
定積分の性質
\begin{eqnarray}
\int_{a}^{b}kf(x)dx&=&k\int_{a}^{b}f(x)dx\\
\\
\int_{a}^{b}{f(x)\pm g(x)}dx&=&\int_{a}^{b}f(x)dx\pm\int_{a}^{b}g(x)dx\\
\\
\int_{a}^{a}f(x)dx&=&0\\
\\
\int_{a}^{b}f(x)dx&=&-\int_{b}^{a}f(x)dx\\
\\
\int_{a}^{b}f(x)dx&=&\int_{a}^{c}f(x)dx+\int_{c}^{b}f(x)dx
\end{eqnarray}
面積の求め方
図1.2の濃い青の範囲の面積Sを考える。
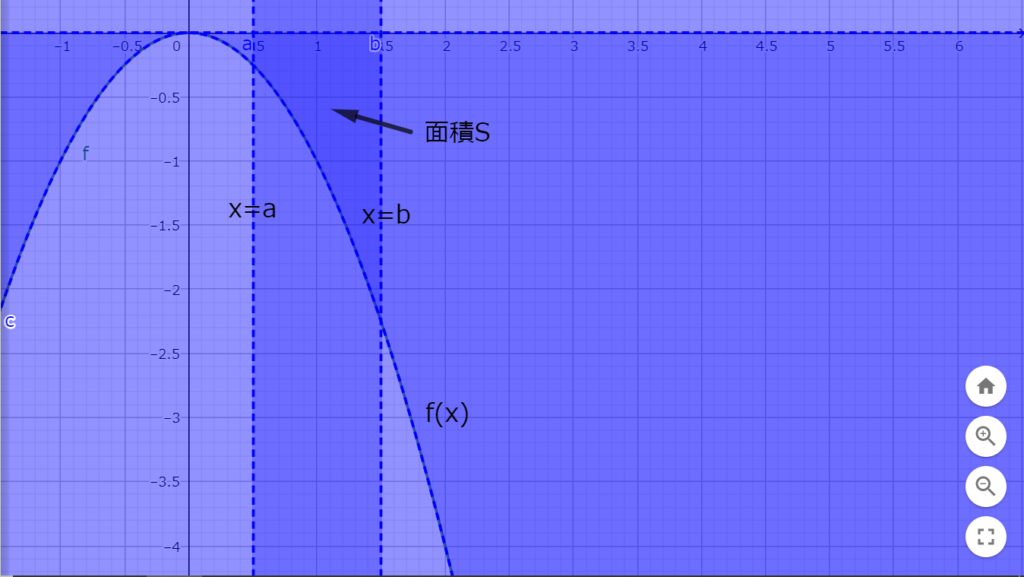 図1.2 x=aからx=bの範囲でf(x)<0を満たす関数f(x)
図1.2 x=aからx=bの範囲でf(x)<0を満たす関数f(x)\(a\leq x\leq b\)では\(f(x)\leq0\)なので積分結果にマイナスをかける必要がある。
\begin{eqnarray}
S=-\int_{a}^{b}f(x)dx
\end{eqnarray}
図1.3の濃い青の範囲の面積Sを考える。
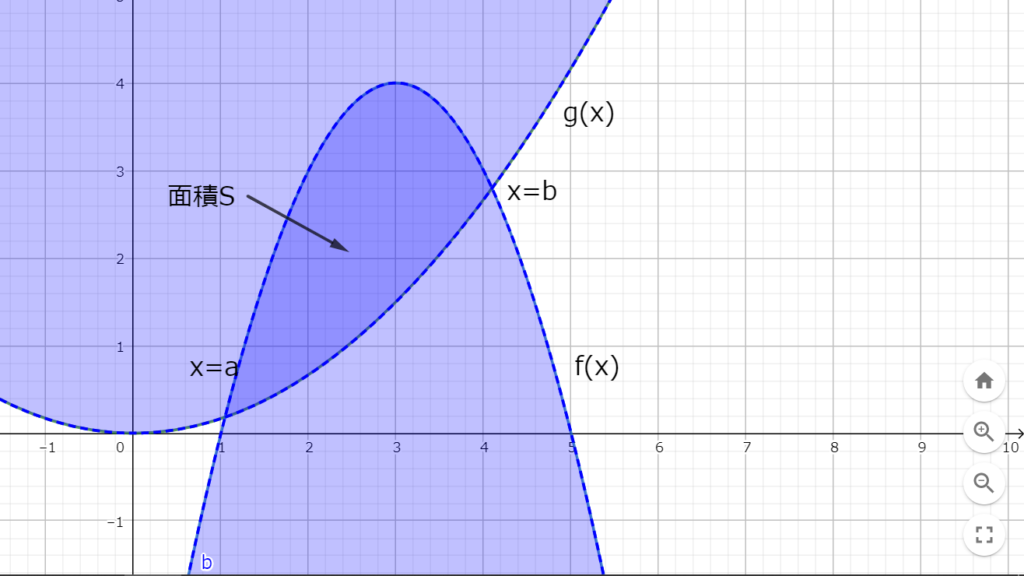 図1.3 関数f(x)と関数g(x)に囲まれた範囲
図1.3 関数f(x)と関数g(x)に囲まれた範囲\(a\leq x\leq b\)の範囲では\(f(x)\geq g(x)\)なので\(f(x)-g(x)\)の積分を行う。
\begin{eqnarray}
\int_{a}^{b}{f(x)-g(x)}dx
\end{eqnarray}
【練習問題はこちら】

