問題
問1
以下のベクトルがあるとする。
\begin{eqnarray}
\vec{a}&=&(9,3)\\
\\
\vec{b}&=&(-1,-2)\\
\\
\vec{c}&=&\vec{a}+t\vec{b}
\end{eqnarray}
この時、\(|\vec{c}|\)の値の最小値を求めよ。
【解答はこちら】
問2
以下のベクトルがあるとする。
\begin{eqnarray}
\vec{a}&=&(4,2)\\
\\
\vec{b}&=&(3,-1)\\
\\
\vec{x}&=&(p,q)
\end{eqnarray}
この時、以下の条件を満たす時の\(p,q\)の値を求めよ。
\begin{eqnarray}
\vec{x}//\vec{b}-\vec{a}\\
\\
\vec{x}-\vec{b}\perp\vec{a}
\end{eqnarray}
【解答はこちら】
問3
以下のベクトルがあるとする。
\begin{eqnarray}
|\vec{a}|&=&2\\
\\
|\vec{b}|&=&1\\
\\
\vec{a}\cdot\vec{b}&=&-1
\end{eqnarray}
この時、以下の(1)、(2)の問に答えよ。
(1)
\(\vec{a}+t\vec{b}\)の最小値とその時のtを求めよ。
(2)
(1)で求めた\(t\)の値を\(t_0\)とする時、以下のことを示せ。
\begin{eqnarray}
\vec{a}+t_0\vec{b}\perp\vec{b}
\end{eqnarray}
【解答はこちら】
問4
平行四辺形ABCDの対角線BDの三等分線をBに近い方からE,Fとする。
この時、四角形AECFは平行四辺形であることを証明せよ。
【解答はこちら】
問5
△ABCにおいてABを3:1に内分する点をD、ACを2:3に内分する点をE、BEとCDの交点をPとする。
また、以下のようにベクトルを定義する。
\begin{eqnarray}
\vec{AB}&=&\vec{b}\\
\\
\vec{AC}&=&\vec{c}
\end{eqnarray}
この時、\(\vec{AP}\)を\(\vec{b}\)、\(\vec{c}\)で表わせ。
【解答はこちら】
解答
問1の解答 絶対値を二次関数にする
【問題はこちら】
\(\vec{c}\)を計算すると以下の様になる。
\begin{eqnarray}
\vec{c}=(9-t,3-2t)
\end{eqnarray}
よって、\(|\vec{c}|\)は以下のように計算できる。
\begin{eqnarray}
|\vec{c}|&=&\sqrt{\left(9-t\right)^2+\left(3-2t\right)^2}\\
\\
&=&\sqrt{5t^2-30t+90}\\
\\
&=&\sqrt{5\left(t-3\right)^2+45}
\end{eqnarray}
よって、\(t=3\)の時、\(|\vec{c}|\)は最小値\(3\sqrt{5}\)を取る。
関連単元
【二次関数の性質】
問2の解答 ベクトルの並行条件と垂直条件を確認する
【問題はこちら】
ベクトル\(\vec{x}\)と\(\vec{b}-\vec{a}\)が平行であることを示すには互いのベクトルが定数倍である必要がある。
ここで\(\vec{b}-\vec{a}\)は以下である。
\begin{eqnarray}
\vec{b}-\vec{a}=\left(-1,-3\right)
\end{eqnarray}
よって、係数\(k\)を使って以下の条件を考える。
\begin{eqnarray}
\vec{b}-\vec{a}=k\vec{x}\\
↓\\
p=-k\\
q=-3k\\
↓\\
q=3p\tag{2.1}
\end{eqnarray}
次に\(\vec{x}-\vec{b}\)と\(\vec{a}\)が垂直であるということを考える。
ここで、\(\vec{x}-\vec{b}\)は以下である。
\begin{eqnarray}
\vec{x}-\vec{b}=\left(p-3,q+1\right)
\end{eqnarray}
また、垂直なベクトル同士の内積は0である。
よって、以下の関係が成り立つ。
\begin{eqnarray}
\left(\vec{x}-\vec{b}\right)\cdot\vec{a}&=&4\left(p-3\right)+2\left(q+1\right)\\
\\
&=&4p+2q\\
\\
&=&0\\
↓\\
2p+q&=&5\tag{2.2}
\end{eqnarray}
ここで、式2.2に式2.1の\(q\)の値を代入すると\(p\)の値を求めることができる。
よって、\(p,q\)の値は以下の様になる。
\begin{eqnarray}
\left(p,q\right)=\left(1,3\right)
\end{eqnarray}
問3の解答 \(|\vec{a}+t\vec{b}|\)の二乗を計算してtの二次関数を作る
【問題はこちら】
(1)
まず、\(|\vec{a}+t\vec{b}|>0\)なので\(|\vec{a}+t\vec{b}|^2\)を計算しても\(t\)による大小関係が崩れることはない。
よって、\(|\vec{a}+t\vec{b}|^2\)の最小値を計算する。
\begin{eqnarray}
|\vec{a}+t\vec{b}|^2&=&|\vec{a}|^2+2t\vec{a}\cdot\vec{b}+t^2|\vec{b}|\\
\\
&=&t^2-2t+4\\
\\
&=&\left(t-1\right)^2+3
\end{eqnarray}
以上より\(|\vec{a}+t\vec{b}|^2\)は\(t\)の二次関数であることが分かり、平方完成から\(t=1\)の時に最小値\(3\)を取ることが分かる。
よって、\(|\vec{a}+t\vec{b}|\)の最小値は\(t=1\)の時\(\sqrt{3}\)を取ることが分かる。
(2)
ここで、\(t_0=1\)なので\(\left(\vec{a}+\vec{b}\right)\perp\vec{b}\)(内積が0)になることを示せば良い。
\begin{eqnarray}
\left(\vec{a}+\vec{b}\right)\cdot\vec{b}&=&\vec{a}\cdot\vec{b}+|\vec{b}|^2\\
\\
&=&-1+1\\
\\
&=&0
\end{eqnarray}
よって、\(\left(\vec{a}+\vec{b}\right)\perp\vec{b}\)が証明された。
問4の解答 向かい合う辺がそれぞれ平行であることを示す
【問題はこちら】
図4.1の様に平行四辺形ABCDと四角形AECFがある。
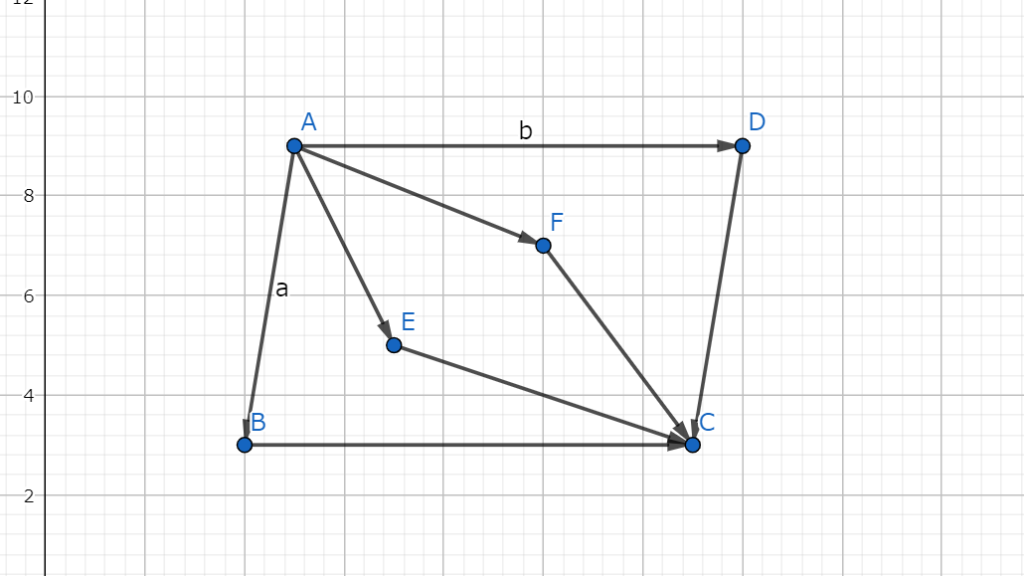 図4.1 平行四辺形ABCDと対角線BDを3つに均等に内分する点Eと点F
図4.1 平行四辺形ABCDと対角線BDを3つに均等に内分する点Eと点Fこの時、\(AE//FC\)と\(AF//EC\)を示せば良い。
つまり、\(\vec{AE}=k\vec{FC}\)と\(\vec{AF}=l\vec{FC}\)を示せば良い。
ここで、\(\vec{AB}=\vec{a}\)と\(\vec{AD}=\vec{b}\)とする。
これから計算するベクトルを\(\vec{a}\)と\(\vec{b}\)で表す。
まず、\(\vec{AF}\)を計算する。
\begin{eqnarray}
\vec{AF}&=&\vec{AB}+\frac{1}{3}\left(\vec{BD}\right)\\
\\
&=&\vec{AB}+\frac{1}{3}\left(\vec{AD}-\vec{AB}\right)\\
\\
&=&\frac{2}{3}\vec{AB}+\frac{1}{3}\vec{AD}\\
\\
&=&\frac{2}{3}\vec{a}+\frac{1}{3}\vec{b}\tag{4.1}
\end{eqnarray}
次に\(\vec{FC}\)を計算する。
\begin{eqnarray}
\vec{FC}&=&\vec{AC}-\vec{AF}\\
\\
&=&\vec{AD}+\vec{DC}-\left(\vec{AB}+\frac{2}{3}\vec{BD}\right)\\
\\
&=&\vec{b}+\vec{a}-\vec{a}-\frac{2}{3}\left(\vec{AD}-\vec{AB}\right)\\
\\
&=&\vec{b}-\frac{2}{3}\vec{b}+\frac
{2}{3}\vec{a}\\
\\
&=&\frac{2}{3}\vec{a}+\frac{1}{3}\vec{b}\tag{4.2}
\end{eqnarray}
式4.1と式4.2より\(\vec{AF}\)と\(\vec{FC}\)は平行であることが分かった。
次に\(\vec{AF}\)を計算する。
\begin{eqnarray}
\vec{AF}&=&\vec{AB}+\frac{2}{3}\vec{BD}\\
\\
&=&\vec{a}+\frac{2}{3}\left(\vec{AD}-\vec{AB}\right)\\
\\
&=&\vec{a}+\frac{2}{3}\vec{b}-\frac{2}{3}\vec{a}
\\
&=&\frac{1}{3}\vec{a}+\frac{2}{3}\vec{b}\tag{4.3}
\end{eqnarray}
次に\(\vec{EC}\)を計算する。
\begin{eqnarray}
\vec{EC}&=&\vec{AC}-\vec{AE}\\
\\
&=&\vec{AB}+\vec{BC}-\left(\vec{AB}+\frac{1}{3}\vec{BD}\right)\\
\\
&=&\vec{b}-\frac{1}{3}\left(\vec{AD}-\vec{AB}\right)\\
\\
&=&\frac{1}{3}\vec{a}+\frac{2}{3}\vec{b}\tag{4.4}
\end{eqnarray}
式4.3と式4.4より\(\vec{AF}//\vec{EC}\)であることが分かった。
よって、\(\vec{AF//\vec{EC}}\)かつ\(\vec{AE}//\vec{FC}\)より四角形AECFは平行四辺形であることが証明された。
問5の解答 \((1-t)\)と\(t\)に内分する点と\(1-s\)と\(s\)に内分する点を考える
【問題はこちら】
図5.1のような三角形を考える。
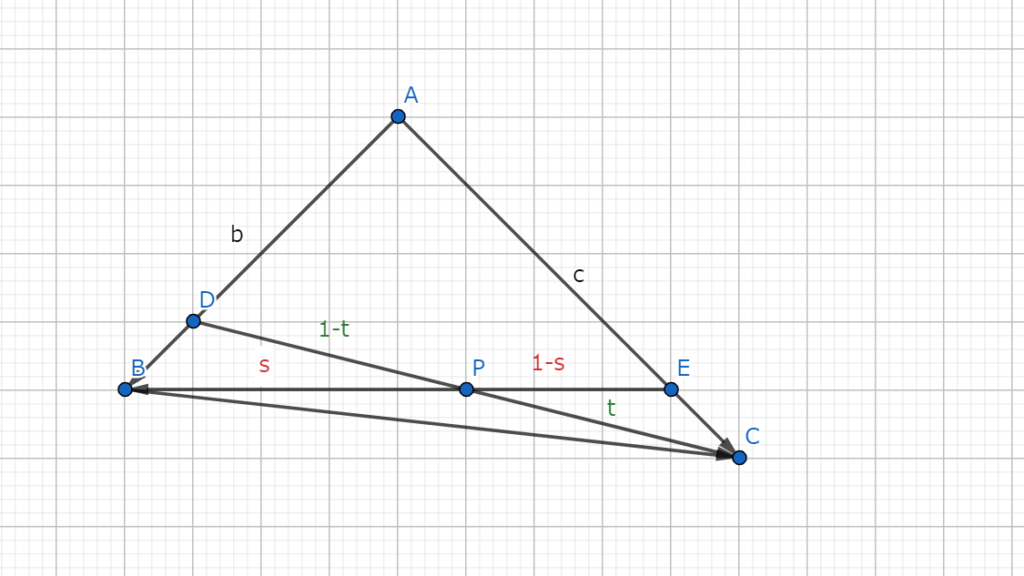 図5.1 三角形ABCと辺ABを3:1に内分する点Dと辺ACを5:1に内分する点E
図5.1 三角形ABCと辺ABを3:1に内分する点Dと辺ACを5:1に内分する点Eこの時、点Pは辺BCを\(s:1-s\)に内分する点と考える。
すると、三角形ABEに注目した時に\(\vec{AP}\)は\(\vec{b}\)と\(\vec{c}\)を使って以下のように表すことができる。
\begin{eqnarray}
\vec{AP}&=&\left(1-s\right)\vec{b}+s\frac{2}{5}\vec{c}\tag{5.1}
\end{eqnarray}
また、点P は辺CDを\(t:1-t\)に内分する点と考える。
すると、三角形ADCに注目した時に\(\vec{AP}\)は\(\vec{b}\)と\(\vec{c}\)を使って以下のように表すことができる。
\begin{eqnarray}
\vec{AP}&=&t\frac{3}{4}\vec{b}+\left(1-t\right)\vec{c}\tag{5.2}
\end{eqnarray}
式5.1と式5.2のベクトル\(\vec{b}\)と\(\vec{c}\)の係数を比較すると\(s\)と\(t\)についての連立方程式を以下のように作ることができる。
\begin{eqnarray}
\frac{3}{4}t&=&1-s\\
\\
1-t&=&\frac{2}{5}s
\end{eqnarray}
以上の連立方程式を解くと\(s,t\)は以下のようになる。
\begin{eqnarray}
\left(s,t\right)=\left(\frac{5}{14},\frac{6}{7}\right)
\end{eqnarray}
よって、\(\vec{AP}\)は以下の様になる。
\begin{eqnarray}
\vec{AP}=\frac{9}{14}\vec{b}+\frac{1}{7}\vec{c}
\end{eqnarray}
関連単元
【内分する点とは】

