問題
問1
曲線\(f(x)\)は点(1,-1)を通り、曲線上の各点(x,y)における接線の傾きは以下の式で表される。
$$3\left(x^2-1\right)$$
この時の曲線の方程式を求めよ。
【解答はこちら】
問2
以下の3つの等式を満たす二次関数\(f(x)\)を求めよ。
\begin{eqnarray}
\int_{-1}^{1}f(x)dx&=&0\tag{①}\\
\\
\int_{0}^{2}f(x)dx&=&10\tag{②}\\
\\
\int_{-1}^{1}xf(x)dx&=&\frac{4}{3}\tag{③}
\end{eqnarray}
【解答はこちら】
問3
以下の関数\(f(x)\)の最大値と最小値とその時のxを求めよ。
\begin{eqnarray}
f(x)=\int_{0}^{x}\left(t-1\right)\left(t+3\right)dt\\
(0\leq x\leq4)
\end{eqnarray}
【解答はこちら】
問4
以下の条件を満たす\(f(x),g(x)\)を求めよ。
\begin{eqnarray}
f(x)+\int_{0}^{x}g(t)dt&=&3x^2+2x+1\tag{式4.1}\\
\\
\frac{d}{dx}f(x)&=&g(x)+4x^2\tag{式4.2}
\end{eqnarray}
【解答はこちら】
問5
以下の放物線がある。
$$y=x^2-4x+3$$
この放物線上の点(4,3)、(0,3)における接線と放物線で囲まれた部分の面積を求めよ。
【解答はこちら】
問6
以下の放物線がある。
$$y=x^2+4$$
この放物線上の点Pにおける接線と放物線\(y=x^2\)で囲まれた部分の面積Sは点Pの選び方に関係なく一定であることを示せ。
【解答はこちら】
解答
問1の解答 積分定数を求める
【問題はこちら】
\(f'(x)\)は以下の様になる。
\begin{eqnarray}
f^{\prime}(x)=3\left(x^2-1\right)
\end{eqnarray}
よって、曲線の方程式\(f(x)\)は以下の様になる。
\begin{eqnarray}
f(x)&=&\int f^{\prime}(x)dx\\
\\
&=&x^3-3x+C (Cは定数)
\end{eqnarray}
この時、曲線は点(1,-1)を通るので以下の等式が成り立つ。
\begin{eqnarray}
f(x=1)=-2+C=-1\\
↓\\
C=1
\end{eqnarray}
よって、曲線の関数は以下となる。
\begin{eqnarray}
f(x)=x^3-3x+1
\end{eqnarray}
問2の解答 条件から連立方程式を解く
【問題はこちら】
まず、\(f(x)\)を以下の関数と置く。
\begin{eqnarray}
f(x)=ax^2+bx+c
\end{eqnarray}
ここで、①、②、③の条件を使っていく。
①より、
\begin{eqnarray}
&&\int_{-1}^{1}\left(ax^2+bx+c\right)dx\\
\\
&=&\left[\frac{a}{3}x^3+\frac{b}{2}x^2+cx\right]_{-1}^{1}\\
\\
&=&\frac{2}{3}a+2c=0\tag{④}
\end{eqnarray}
②より、
\begin{eqnarray}
&&\int_{0}^{2}\left(ax^2+bx+c\right)dx\\
\\
&=&\left[\frac{a}{3}x^3+\frac{b}{2}x^2+cx\right]_{0}^{2}\\
\\
&=&\frac{8}{3}a+2b+2c=10\tag{⑤}
\end{eqnarray}
③より、
\begin{eqnarray}
&&\int_{-1}^{1}\left(ax^3+bx^2+cx\right)dx\\
\\
&=&\left[\frac{a}{4}x^4+\frac{b}{3}x^3+\frac{c}{2}x^2\right]_{-1}^{1}\\
\\
&=&\frac{2}{3}b=\frac{4}{3}\tag{⑥}
\end{eqnarray}
⑥より
\begin{eqnarray}
b=2
\end{eqnarray}
\(b\)を⑤に代入すると以下になる。
\begin{eqnarray}
\frac{8}{3}a+2c=6\tag{⑤’}
\end{eqnarray}
④、⑤’より
\begin{eqnarray}
a=3,c=-1
\end{eqnarray}
よって、関数\(f(x)\)は以下になる。
\begin{eqnarray}
f(x)=3x^2+2x-1
\end{eqnarray}
問3の解答 \(f(x)\)の外形を調べる
【問題はこちら】
\(f(x)\)を計算する。
\begin{eqnarray}
f(x)&=&\int_{0}^{x}\left(t-1\right)\left(t-3\right)dt\\
\\
&=&\int_{0}^{x}\left(t^2-4t+3\right)dt\\
\\
&=&\left[\frac{1}{3}t^3-2t^2+3t\right]_0^x\\
\\
&=&\frac{1}{3}x^3-2x^2+3x
\end{eqnarray}
よって、\(f(x)\)の増減表は以下となる。
| $$x$$ | $$0$$ | $$\cdots$$ | $$1$$ | $$\cdots$$ | $$3$$ | $$\cdots$$ | $$4$$ |
| $$f^{\prime}(x)$$ | $$+$$ | $$+$$ | $$0$$ | $$-$$ | $$0$$ | $$+$$ | $$+$$ |
| $$f(x)$$ | $$0$$ | $$↗$$ | $$\frac{4}{3}$$ | $$↘$$ | $$0$$ | $$↗$$ | $$\frac{4}{3}$$ |
よって、\(f(x)\)は図3.1のような外形になる。
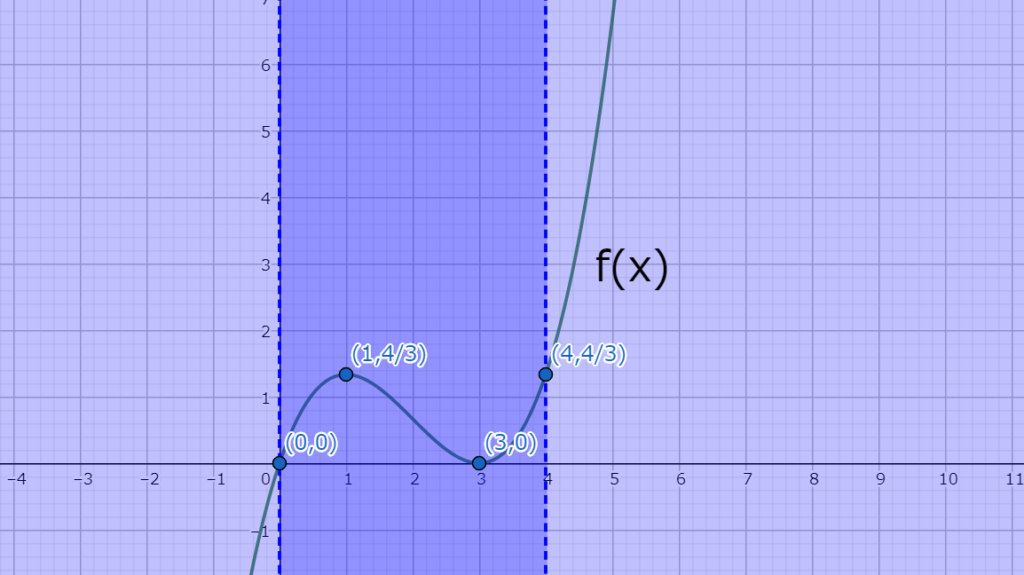 図3.1 f(x)のグラフ
図3.1 f(x)のグラフよって、最大値、最小値は以下となる。
\begin{eqnarray}
最大値&:&f(x=1,4)=\frac{4}{3}\\
\\
最小値&:&f(x=0,3)=0
\end{eqnarray}
問4の解答 \(g(x)\)の積分関数である\(G(x)\)を考える
【問題はこちら】
まず、以下の等式を満たす\(G(x)\)を定義する。
\begin{eqnarray}
\frac{d}{dx}G(x)=g(x)
\end{eqnarray}
この時、\(g(t)\)を積分すると以下になる。
\begin{eqnarray}
\int_{0}^{x}g(t)dt=G(x)-G(0)
\end{eqnarray}
ここで、式4.1を変形して\(f(x)\)に代入する。
\begin{eqnarray}
f(x)&=&3x^2+2x+1-\int_{0}^{x}g(t)dt\\
\\
&=&3x^2+2x+1-G(x)+G(0)
\end{eqnarray}
ここで、求めた\(f(x)\)を式4.2に代入する。
\begin{eqnarray}
&&\frac{d}{dx}\left(3x^2+2x+1-G(x)+G(x)\right)\\
\\
&=&6x+2-g(x)\\
\\
&=&g(x)+4x^2
\end{eqnarray}
よって、g(x)は以下となる。
\begin{eqnarray}
g(x)=-2x^2+3x+1
\end{eqnarray}
また、\(g(x)\)を式4.1に代入すると\(f(x)\)を以下のように計算できる。
\begin{eqnarray}
f(x)&=&3x^2+2x+1-\int_{0}^{x}\left(-2t^2+3t+1\right)dt\\
\\
&=&3x^2+2x+1-\left[-\frac{2}{3}+\frac{2}{3}x^2+x\right]_0^x\\
\\
&=&\frac{2}{3}x^3+\frac{2}{3}+x+1
\end{eqnarray}
問5の解答 接線の交点を中心に積分範囲を分ける
【問題はこちら】
まず、放物線の接線の方程式を求める。
放物線の導関数\(f'(x)\)は以下となる。
\begin{eqnarray}
f^{\prime}(x)=2x-4
\end{eqnarray}
よって、点(4,3)における接線の方程式は以下となる。
\begin{eqnarray}
y-3&=&f^{\prime}(4)\left(x-4\right)\\
↓\\
y&=&4x-13\tag{⑦}
\end{eqnarray}
次に点(0,3)における接線の方程式は以下となる。
\begin{eqnarray}
y-3&=&f^{\prime}(0)x\\
↓\\
y&=&-4x+3\tag{⑧}
\end{eqnarray}
ここで、⑦と⑧の接線の交点のx座標を求める。
\begin{eqnarray}
4x-13=-4x+3\\
↓\\
x=2
\end{eqnarray}
よって、放物線と接線をグラフに描くと図5.1の様になる。
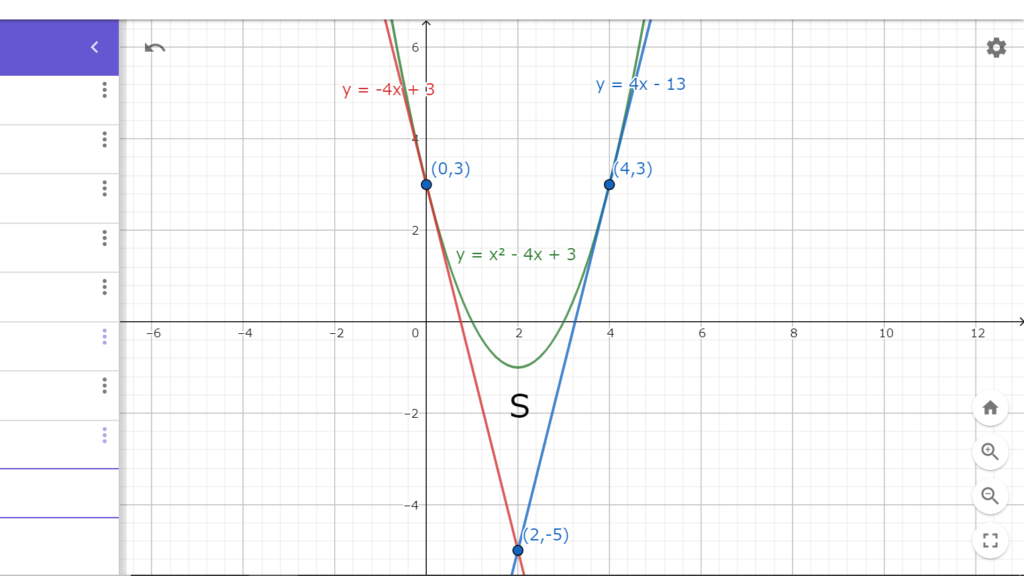 図5.1 f(x)と2つの接線に囲まれた部分の面積S
図5.1 f(x)と2つの接線に囲まれた部分の面積S図5.1を見て分かるように求める面積Sは接線の交点を境に分かれている。
よって、積分範囲を左側で⑦の接線の方程式との面積を計算して、右側で⑧の接線の方程式との面積を計算する。
\begin{eqnarray}
S&=&\int_{0}^{2}\left(f(x)+4x-3\right)dx\\
&&+\int_{2}^{4}\left(f(x)-4x+13\right)\\
\\
&=&\int_{0}^{2}x^2dx+\int_{2}^{4}\left(x^2-8x+16\right)\\
\\
&=&\left[\frac{1}{3}x^3\right]_0^2+\left[\frac{1}{3}x^3-4x^2+16x\right]_2^4\\
\\
&=&\frac{16}{3}
\end{eqnarray}
問6の解答 面積Sが点Pのx座標に依らないことを示す
【問題はこちら】
面積が点Pのx座標に依らないことを示す。
まず、\(f(x),g(x)\)を以下のように置く。
\begin{eqnarray}
f(x)&=&x^2+4\\
\\
g(x)&=&x^2
\end{eqnarray}
最初に\(f(x)\)の接線の方程式を求める。
導関数\(f'(x)\)は以下となる。
\begin{eqnarray}
f'(x)=2x
\end{eqnarray}
点\(P(p,p^2+4)\)とすると接線の方程式は以下となる。
\begin{eqnarray}
y=2px-p^2+4
\end{eqnarray}
次に接線と\(g(x)\)の交点を求める。
\begin{eqnarray}
x^2=2px-p^2+4\\
↓\\
x^2-2px+p^2-4=0\\
↓\\
\left(x-p-2\right)\left(x-p+2\right)\\
\\
x=p\pm2
\end{eqnarray}
よって、\(f(x),g(x)\)と接線の関係は図6.1の様になる。
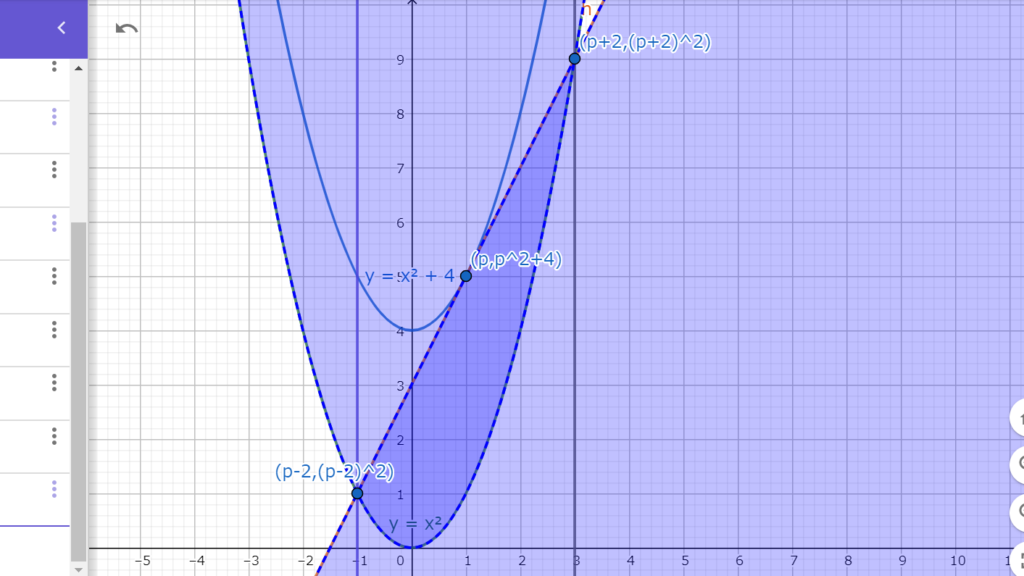 図6.1 f(x)=x^2+4とg(x)=x^2のグラフとf(x)の接線とg(x)に囲まれた部分
図6.1 f(x)=x^2+4とg(x)=x^2のグラフとf(x)の接線とg(x)に囲まれた部分ここで、接線とg(x)で囲まれた部分に注目する。
まず、p-2とp+2の間で接線とx軸に囲まれた部分を見ると台形の形をしている。
この台形の面積を求めてから、g(x)とx軸で囲まれた面積を引く方法を取る。
最初に台形の面積を求める。
台形の面積S1は以下のように計算できる。
\begin{eqnarray}
S_1&=&\frac{1}{2}4\left(\left(p+2\right)^2+\left(p-2\right)^2\right)\\
\\
&=&4p^2+16
\end{eqnarray}
次にg(x)とx軸に囲まれた面積S2をp-2からp+2まで計算する。
\begin{eqnarray}
S_2&=&\int_{p-2}^{p+2}x^2dx\\
\\
&=&\left[\frac{1}{3}x^3\right]_{p-2}^{p+2}\\
\\
&=&\frac{1}{3}\left(\left(p+2\right)^3-\left(p-2\right)^3\right)\\
\\
&=&4p^2+\frac{16}{3}
\end{eqnarray}
よって、面積Sは以下の様になる。
\begin{eqnarray}
S&=&4p^2+16-\left(4p^2+\frac{16}{3}\right)\\
\\
&=&\frac{32}{3}
\end{eqnarray}
よって、面積Sはpに依らず一定であることが分かる。
よって、面積Sは点Pに依らず一定である。

