問題
問1
以下の関係が成り立つとする。
$$2^x-2^{-x}=5\tag{式1.1}$$
この時、以下の値を求めよ。
$$2^x+2^{-x}$$
【解答はこちら】
問2
以下の関係が成り立つとする。
$$a^{2x}=5,a>0$$
この時、以下の値を求めよ。
$$a^x+a^{-x}$$
【解答はこちら】
問3
次の方程式を解け。
$$4^x-64=3・2^{x+2}\tag{式3.1}$$
【解答はこちら】
問4
次に式を\(x^m\)の形に表せ。
$$a^{\log_a x},a>0,x>0\tag{式4.1}$$
【解答はこちら】
問5
以下の関係が成り立つとする。
$$2^x=3^y=6^z,xyz\neq0$$
この時、y,zをxで表わせ。
また、以下の等式が成り立つことも証明せよ。
$$\frac{1}{x}+\frac{1}{y}=\frac{1}{z}\tag{式5.1}$$
【解答はこちら】
問6
次の方程式を解け。
$$\left(\log_2 x\right)^2-\log_2 x^2-3=0\tag{式6.1}$$
【解答はこちら】
問7
以下の関数の最大値を求めよ。
$$y=\log_2\left(-x^2+3x-2\right)\tag{式7.1}$$
【解答はこちら】
解答
問1の解答 求める値をkと置く
【問題はこちら】
最初に式1.1の両辺を二乗する。
\begin{eqnarray}
\left(2^x-2^{-x}\right)^2&=&2^{2x}-2+2^{-2x}\\
&=&25\\
\\
2^{2x}+2^{-2x}=27\tag{①}
\end{eqnarray}
次に以下の様に与えられた値をkと置く。
$$k=2^x+2^{-x}$$
そして、kの二乗を計算する。
\begin{eqnarray}
k^2&=&2^{2x}+2^{-2x}+2\\
&=&27+2\\
&=&29
\end{eqnarray}
よって、kの値は以下となる。
$$k=\sqrt{29}$$
問2の解答 与えられた値をkと置く
【問題はこちら】
与えられた値をkと置くと以下の様になる。
$$k=a^x+a^{-x}$$
次にkの二乗を計算する。
\begin{eqnarray}
k^2&=&a^{2x}+a^{-2x}+2\\
&=&5+\frac{1}{5}+2\\
&=&\frac{36}{5}
\end{eqnarray}
よって、求めるkは以下になる。
$$k=\frac{6}{\sqrt{5}}$$
問3の解答 \(k=2^x\)と置く
【問題はこちら】
式3.1において\(k=2^x\)と置いてkの二次方程式にする。
\begin{eqnarray}
\left(2^x\right)^2-3\cdot4\cdot2^x-64\\
\\
k^2-12k-64=0\\
\\
\left(k-16\right)\left(k+4\right)=0
\\
k=16,-4
\end{eqnarray}
ここで、\(k=2^x\)なので正の値しか取らない。
よって、求めるxは以下となる。
\begin{eqnarray}
2^x=16\\
\\
x=4
\end{eqnarray}
問4の解答 対数の定義に則る
【問題はこちら】
以下の様にpを置く。
$$p=\log_a x\tag{式4.2}$$
すると、式4.1は以下のように書ける。
$$(式4.1)=a^p$$
次に式4.2を対数の定義に則って指数関数の形に直すと以下の様になる。
$$a^p=x\tag{式4.3}$$
式4.2、式4.3より、式4.1は以下のように表せる。
$$(式4.1)=x$$
問5の解答 両辺をlogで取る
【問題はこちら】
まず、以下の等式を考える。
$$2^x=3^y\tag{式5.2}$$
式5.2の両辺を\(log_3\)で取ると以下の様にyをxで表すことができる。
\begin{eqnarray}
\log_3 2^x=\log_3 3^y\\
\\
x\log_3 2=y\log_3 3\\
\\
y=x\log_3 2
\end{eqnarray}
次に以下の等式を考える。
$$2^x=6^z\tag{式5.3}$$
式5.3の両辺を\(log_6\)で取ると以下のようにzをxで表すことができる。
\begin{eqnarray}
\log_6 2^x=\log_6 6^z\\
\\
x\log_6 2=z\log_6 6\\
\\
z=x\log_6 2
\end{eqnarray}
次に式5.1を証明する。
以下の式を計算していく。
\begin{eqnarray}
\frac{1}{x}+\frac{1}{y}&=&\frac{1}{x}+\frac{1}{x\log_3 2}\\
\\
&=&\frac{1}{x}\left(\frac{1+\log_3 2}{\log_3 2}\right)\\
\\
&=&\frac{1}{x}\left(\frac{\log_3 6}{\log_3 2}\right)\\
\\
&=&\frac{1}{x}\left(\frac{1}{\frac{\log_3 2}{\log_3 6}}\right)\\
&=&\frac{1}{x}\frac{1}{\log_6 2}\\
&=&\frac{1}{z}
\end{eqnarray}
問6の解答 対数をkと置いてkの二次方程式にする
【問題はこちら】
以下の様に対数をkと置く。
$$k=\log_2 x$$
以上から式6.1をkの二次方程式で表し計算すると以下の様になる。
\begin{eqnarray}
(式6.1)=k^2-2k-3=0\\
\\
\left(k-3\right)\left(k+1\right)=0\\
\\
k=3,-1\\
\\
→\log_2 x=3,-1\\
x=8,\frac{1}{2}
\end{eqnarray}
問7の解答 yはlogの中の関数に対する増加関数である
【問題はこちら】
まず、以下を式7.2と置く。
$$-x^2+3x-2\tag{式7.2}$$
式7.2は真数なので正の値を取る。
よって、以下の不等式が成り立つ。
$$-x^2+3x-2>0$$
この不等式を解くと以下の様になる。
\begin{eqnarray}
\left(x-1\right)\left(x-2\right)<0\\
\\
1< x<2
\end{eqnarray}
ここで、式7.1について考えてみる。
式7.1は式7.2についての増加関数である。
なぜなら、式7.1の底は2であり1より大きいからである。
つまり、図7.1の様に式7.2が大きくなるほど式7.1も大きくなる。
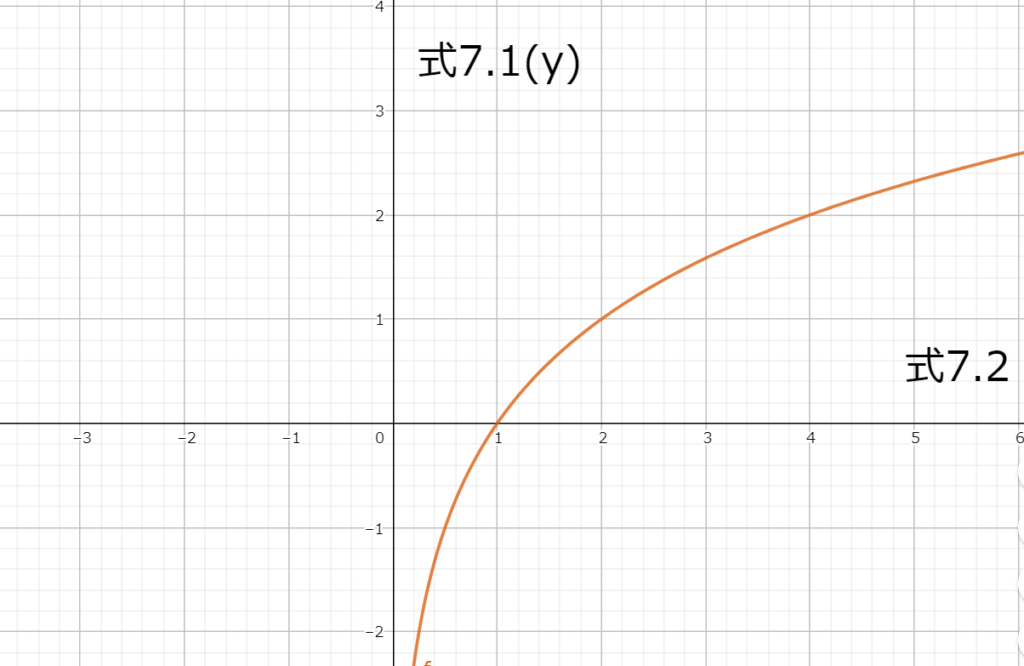
よって、式7.1の最大値は式7.2が最大値を取る時に値を取る。
なので、式7.1の最大値を考える。
式7.2を平方完成すると以下の様になる。
$$(式7.2)=-\left(x-\frac{3}{2}\right)^2+\frac{1}{4}$$
よって、式7.2はx=3/2の時最大値1/4を取る。
よって、式7.1の最大値は以下になる。
\begin{eqnarray}
y_{\left(x=\frac{3}{2}\right)}&=&\log_2 \frac{1}{4}\\
\\
&=&-2
\end{eqnarray}

