指数
指数の性質
指数法則の公式
指数の計算の法則について以下に示す。
\begin{eqnarray}
a^r×a^s&=&a{r+s}\\
\\
\frac{a^r}{a^s}&=&a{r-s}\\
\\
\left(a^r\right)^s&=&a^{rs}\\
\\
\left(ab\right)^r&=&a^rb^r
\end{eqnarray}
累乗根の性質
以下に累乗根の性質について示す。
\begin{eqnarray}
\sqrt[n]{a}\sqrt[n]{b}&=&\sqrt[n]{ab}\\
\\
\frac{\sqrt[n]{a}}{\sqrt[n]{b}}&=&\sqrt[n]{\frac{a}{b}}\\
\\
\left(\sqrt[n]{a}\right)^m&=&\sqrt[n]{a^m}\\
\\]
\sqrt[m]{\sqrt[n]{a}}&=&\sqrt[mn]{a}
\end{eqnarray}
指数関数
指数関数は以下のような関数である。
$$y=a^x$$
この時、指数関数はaの値によって関数の形が変わる。
$$$$0< a<1$$
< a<1$$
< a<1$$
$$0< a<1$$
< a<1$$図1.1のような関数になる。
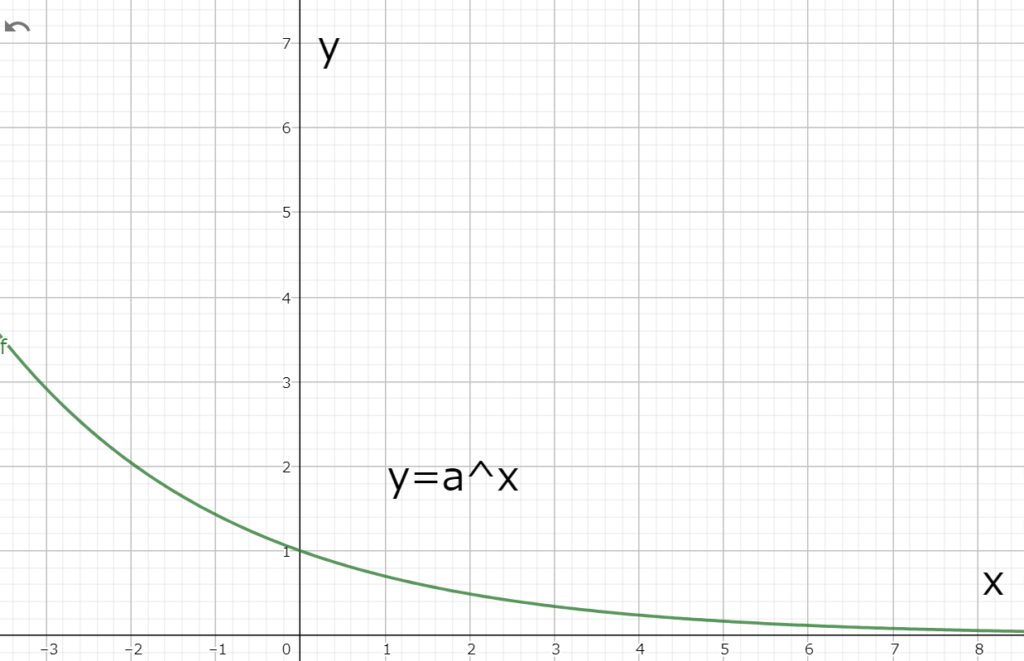図1.1 0<a<1の時のy=a^xのグラフこの関数はxが増加するにつれて常にyが減少しているので減少関数と呼ぶ。
$< a$$
図1.2のような関数になる。
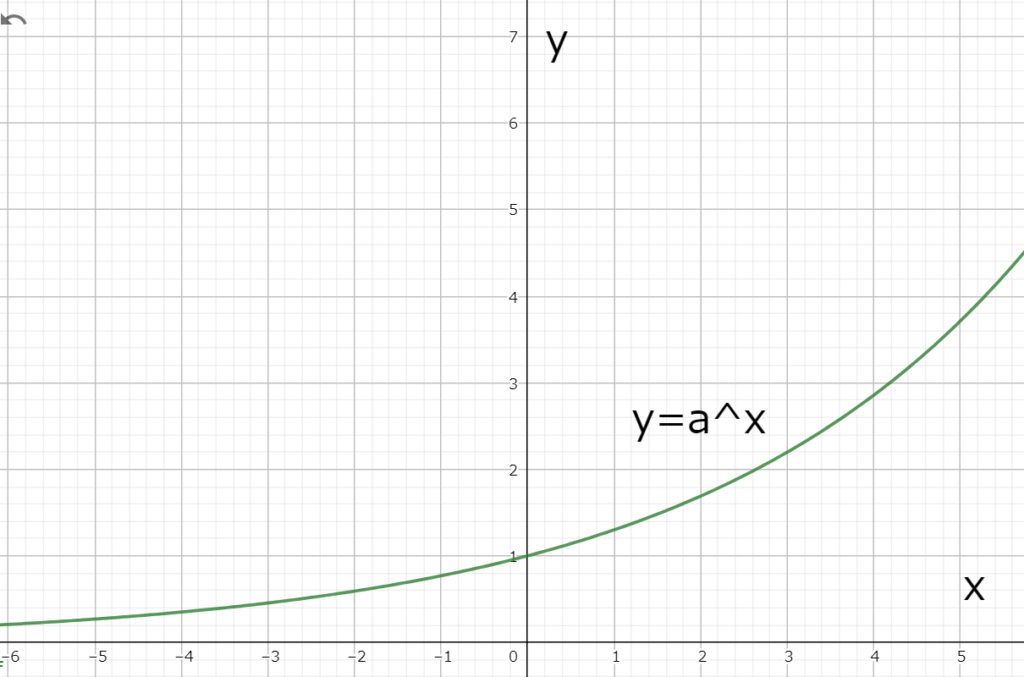図1.2 １＜aの時のy=a^xのグラフこの関数はxが増加するにつれて常にyが増加しているので増加関数と呼ぶ。
対数
対数の性質
以下の条件を満たすa,Mが存在するとする。
\begin{eqnarray}
a>0,a≠1,M>0
\end{eqnarray}
この時、以下の関係を満たす実数pが存在する。
\begin{eqnarray}
M=a^p
\end{eqnarray}
この時、実数pを以下のように表すことができる。
\begin{eqnarray}
p=\log_a M\tag{式1.1}
\end{eqnarray}
式1.1をaを底としたMの対数と呼ぶ。
また、Mを真数と呼ぶ。
対数法則の公式
対数は以下の法則を満たす。
\begin{eqnarray}
\log_a MN&=&\log_a M+\log_a N\\
\\
\log_a \frac{M}{N}&=&\log_a M-\log_a N\\
\\
\log_a M^k&=&k\log_a M\\
\\
(M>0&,&N>0,kは実数)
\end{eqnarray}
また、対数の底を変換する公式は以下になる。
\begin{eqnarray}
\log_a b&=&\frac{\log_c b}{\log_c a}\\
\\
(a>0,b>0&,&c>0,a≠1,c≠1)
\end{eqnarray}
対数関数
対数関数は以下のような関数である。
\begin{eqnarray}
y=\log_a x
\end{eqnarray}
この時、対数関数はaの値によって関数の形が変わる。
$$0< a<1$$
図1.3のような関数となる。
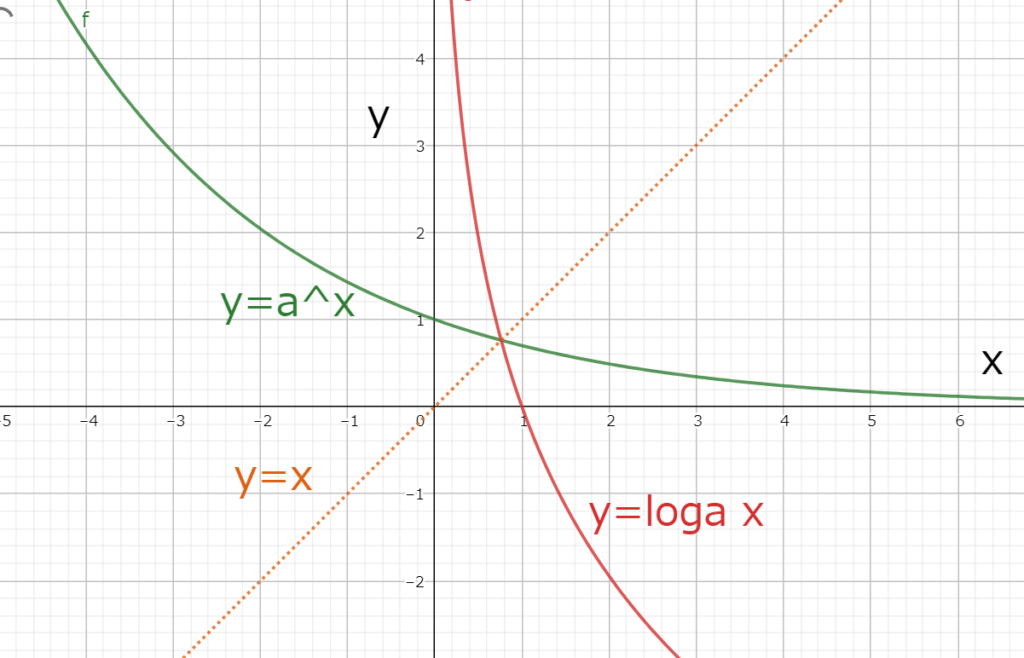図1.3 0<a<1の時のy=loga xとy=a^xのグラフ対数関数はxが増加すると常にyが減少しているので減少関数である。
また、対数関数は以下の指数関数とy=xの直線に対して対称な関数でもある。
$$y=a^x$$
$< a$$
図1.4のような関数となる。
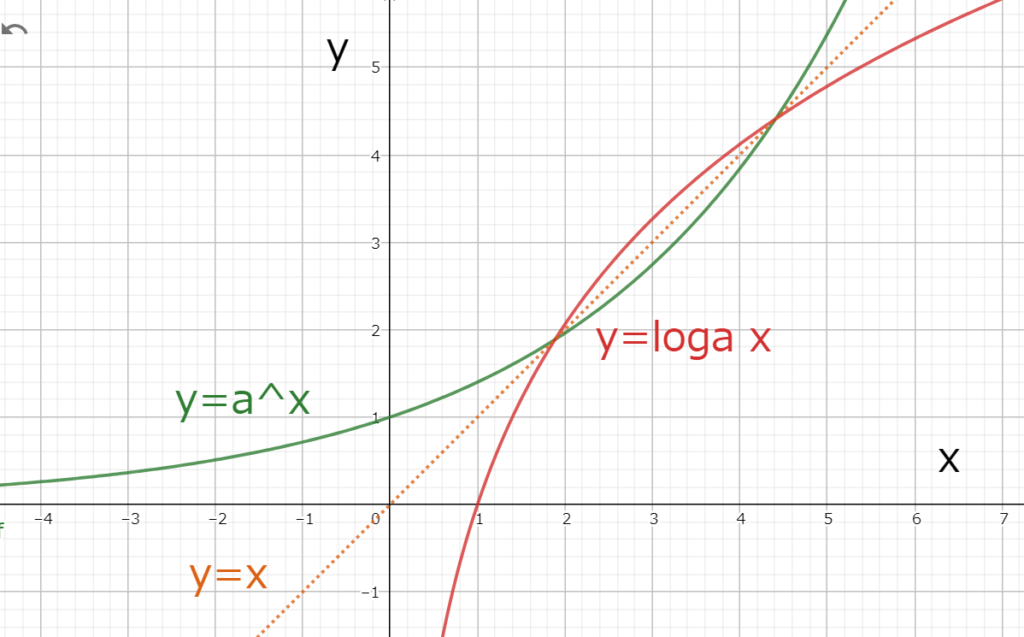図1.4 1<aの時のy=loga xとy=a^xのグラフ対数関数はxが増加すると常にyが増加しているので増加関数である。
また、対数関数は以下の指数関数とy=xの直線に対して対称な関数でもある。
$$y=a^x$$
【練習問題はこちら】
