問題
問1
次の不等式の領域を図示せよ。
$$3x-5y+2\geq0\tag{式1.1}$$
【解答はこちら】
問2
次の不等式の領域を図示せよ。
$$1\leq x^2+y^2\leq9\tag{式2.1}$$
【解答はこちら】
問3
次の不等式の領域を図示せよ。
$$\left(x+y-3\right)\left(x^2+y^2-9\right)<0\tag{式3.1}$$
【解答はこちら】
問4
tの値が変化する時、以下の方程式が通る領域を式で表せ。
$$y=x^2+tx+t^2\tag{式4.1}$$
【解答はこちら】
解答
問1の解答 \(y=ax+b\)の形に式変形する
【問題はこちら】
式1.1を\(y=ax+b\)に変形すると以下になる。
$$y\leq\frac{3}{5}x+\frac{2}{5}$$
図示すると図1.1の様に直線\(y=\frac{3}{5}x+\frac{2}{5}\)よりも小さい領域となる。
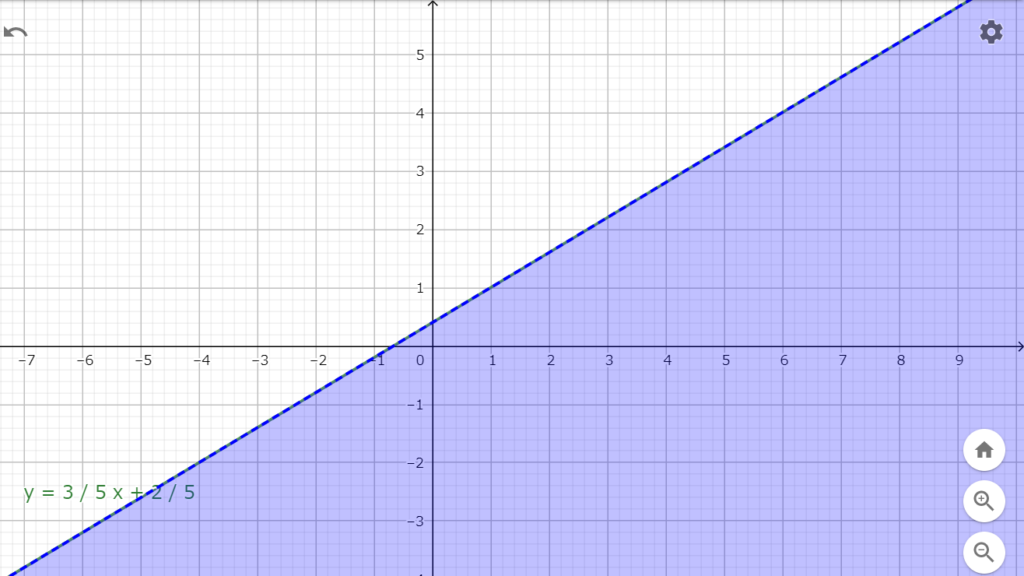 図1.1 y<3/5x+2/5の範囲(青い部分)
図1.1 y<3/5x+2/5の範囲(青い部分)問2の解答 円の領域を考える
【問題はこちら】
\(x^2+y^2\)は円の半径を表す。
よって、円の半径が1以上9以下の領域を式2.1は表す。
つまり、式2.1が表す領域は図2.1のように半径1の円と半径3の円に挟まれた領域となる。
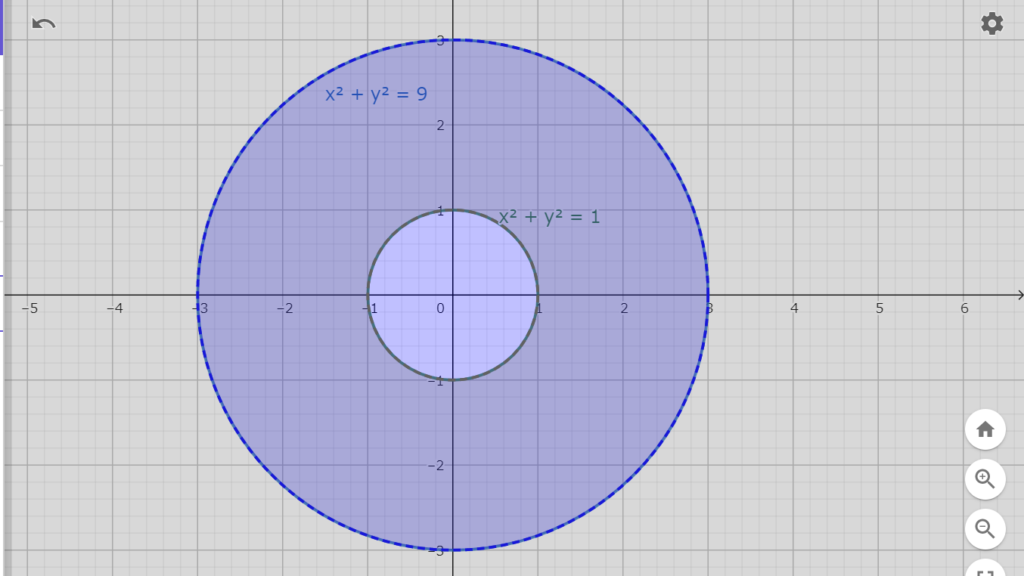 図2.1 半径1と半径3の円に囲まれた範囲(青い部分)
図2.1 半径1と半径3の円に囲まれた範囲(青い部分)問3の解答 2つの因数の積が負になる場合を考える
【問題はこちら】
式3.1は2つの因数からなっている。
これらの因数の積が負である時の領域を式3.1は示している。
つまり、以下の条件を満たす時である。
\begin{eqnarray}
y<-x+3&かつ&x^2+y^2>9\\
&又は&\\
y>-x+3&かつ&x^2+y^2<9
\end{eqnarray}
つまり、直線\(y=-x+3\)よりも大きく半径3の円の内側の場合と、直線よりも小さく半径3の円の外側が式3.1を満たす領域である。
よって、図示すると図3.1-1,3.1-2の様になる。
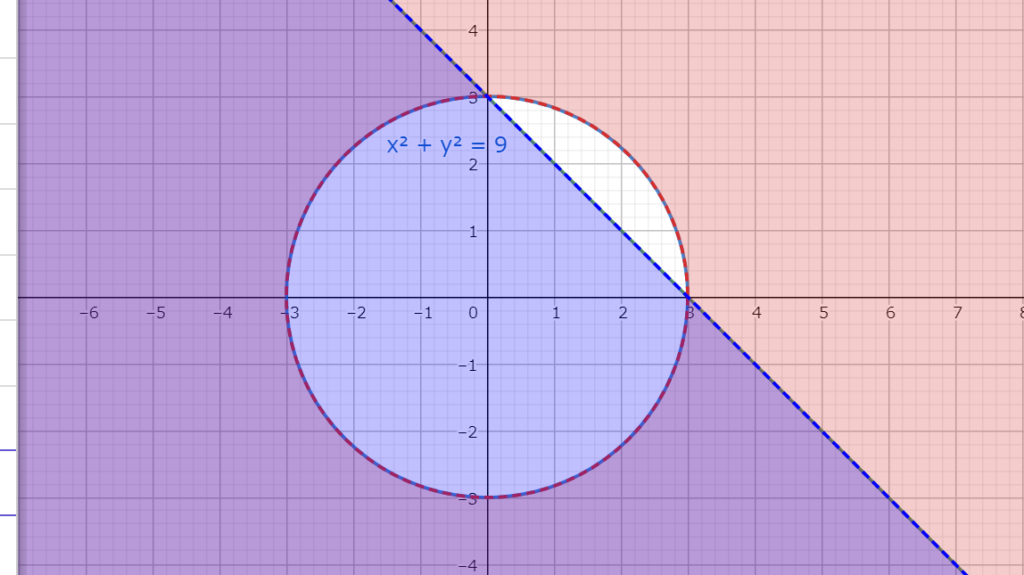 9の範囲(青く赤い部分)” width=”1024″ height=”575″> 図3.1-1 y<-x+3かつx^2+y^2>9の範囲(青く赤い部分)
9の範囲(青く赤い部分)” width=”1024″ height=”575″> 図3.1-1 y<-x+3かつx^2+y^2>9の範囲(青く赤い部分)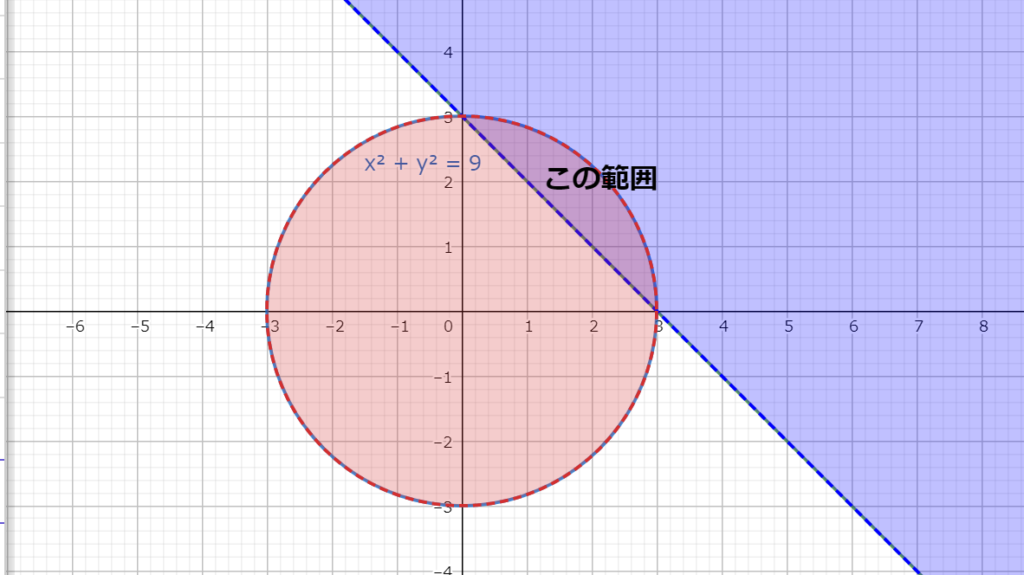 図3.1-2-x+3かつx^2+y^2<9の範囲(青く赤い部分)
図3.1-2-x+3かつx^2+y^2<9の範囲(青く赤い部分)問4の解答 \(t\)を変数として見て、\(t\)が実数解を持つときを考える
【問題はこちら】
式4.1が通る領域においてtを変数として見るとtは実数解を持つことと同義である。
よって、式4.1の\(t\)を変数として見て、\(x,y\)を定数としてみる。
$$t^2+xt+x^2-y=0\tag{①}$$
ここで、\(t\)が実数解を持つときなので①の\(t\)についての判別式\(D\)が\(0\)以上の時を調べる。
\begin{eqnarray}
D&=&x^2-4\left(x^2-y\right)\\
&=&-3x^2+4y\geq0
\end{eqnarray}
よって、以下の領域を示す。
$$y\geq\frac{3}{4}x^2$$

